Keywords
Babylonian mathematics, geometry, algebra, quadratic equations, field plans
§0.1. Abstract
In the late 1920’s the existence of both Old and Late Babylonian mathematical cuneiform texts with solutions to second-degree problems were discovered at O. Neugebauer’s path-breaking history of mathematics seminar in Göttingen. The announcement of the discovery was received with “immense amazement” (Høyrup 2002: 1, fn. 2). In this paper will be discussed, for the first time, the existence of an even older cuneiform text, YBC 3879, a juridical field division document from the Sumerian Ur III period, in which unequivocally appear solutions to a series of second-degree problems. Ironically, a copy of the text in question was published (although without any translation or commentary) in a volume of Miscellaneous Inscriptions in the Yale Babylonian Collection by A. T. Clay in 1915, that is more than a decade before the mentioned sensational discovery at Neugebauer’s seminar!
§0.2. The paper begins in §1 with a thorough discussion of how the full set of length and area numbers appearing in the badly preserved field map on the reverse of the field division document YBC 3879 can be cogently reconstructed, before it goes on to a discussion of the geometric origin in the text of certain second-degree problems. The discussion is followed by a painstaking numerical verification of the solutions given in the text to those problems. It is demonstrated how the lengthy calculations may have been simplified by the use of sexagesimal numbers in place value notation, and how the solutions to the second degree problems may have been obtained geometrically, through manipulations with squares, rectangles, and trapezoids.
§0.3. In §§2-3 some related, but less complicated, examples of Ur III field plan texts are discussed, where given fields are divided into parallel stripes. There is also a discussion of what may be the reason for what seems to be the nearly total absence of known cuneiform mathematical texts from the Sumerian Ur III period.
§0.4. In §4 of the paper, finally, it is shown how a drawing, which can be interpreted as illustrating a second- degree problem of precisely the same kind as the second-degree problems solved in YBC 3879 , appears on IM 58045, a small clay tablet which is securely dated to the Old Akkadian period (five hundred years before the Old Babylonian period), and which is discussed by the author in Amazing Traces (Friberg 2007a: 11.3 a).
The research for this article was generously supported by The Royal Society of Arts and Sciences in Gothenburg.
§1. Ur III field plan texts from Umma, Girsu, and other places Two cuneiform field plan texts from the Sumerian Ur III period in Mesopotamia (around 2100-2000 BC) belonging to the Norwegian Schøyen collection were discussed in Friberg 2007b: ch. 5. One of them, MS 1984, published for the first time already by Allotte de la Fuÿe 1915, is probably from the ancient city Umma, near Lagash-Girsu, while the other one, MS 1850, is new and of unknown provenience, but quite similar to MS 1984.
§1.1. Five further earlier published Ur III field plan texts were discussed briefly in the same chapter of Friberg 2007 (Ist O 1107 and HSM 1659, both from Girsu; Wengler 36, from Umma; VAT 7029 and VAT 7030, both from Drehem).
§1.2. Liverani 1990 contains a list of 32 field plan texts from Ur III, with reproductions of 15 of the field plans. Liverani’s 32 field plan texts include the ones mentioned above, except the new text MS 1850. The list is, of course, not complete. Thus, for instance two more field plan texts from Ur III were published in Zettler 1989.
§1.3. Three new, intimately connected “field division texts” of a new type from Ur III Umma (BM 104801, BM 111022, and BM 110387), two of which contain rudimentary field plans, are being prepared for publication by Farouk Al-Rawi. Discussions with my friend Farouk of the meaning of the various field plan texts from Ur III Umma published by Clay 1915 inspired me to write the present paper. (I would also like to express here my gratitude to Andrew George, who helped me to understand some difficult passages in YBC 3879.)

Figure 1a: Factor diagram for sexagesimal numbers in place value notation.
§1.4. The present paper begins with a careful discussion of YBC 3879 (YOS 1, 24), a text from Ur III Umma with a field plan somewhat similar to the one on MS 1984. Incidentally, YBC 3879 and MS 1984 were both first published in 1915. It is noteworthy that YBC 3879 is absent from Liverani’s list of Ur III field plan texts, although the list includes not only YOS 1, 22, and YOS 1, 23, but also YOS 1, 25, with reproductions of the field plans in all three cases! There is, however, a recent brief but clear discussion of YBC 3879 in Heimpel 2004: §3.2.
§1.5. The absence of YBC 3879 from Liverani’s list is not difficult to understand, since YBC 3879 has several unique features distinguishing it from the Ur III field plan texts mentioned above. Those unique features are:
- While the other Ur III field plans apparently show agricultural fields measured in tens or hundreds or thousands of ikus (1 iku = 100 square ninda = 3600 square meters), or much smaller house plans, the field plan on YBC 3879 shows an orchard (geškiri6), probably a date grove, measuring only a couple of ikus.
- While the other Ur III field plans are inscribed on the flat obverse of their respective clay tablets, with or without a brief summary on the reverse, the field plan on YBC 3879 is (apparently) inscribed on the reverse, with the summary and additional text on the obverse. Indeed, the columns on the text side read left to right, showing that that is the obverse. Maybe the reverse of the clay tablet is the flat side of the tablet in this atypical case just because it was easier to draw the straight lines of the field plan on a flat surface.
- The summary on the obverse of YBC 3879 is followed by a description of how the orchard has been divided into five parallel stripes of equal area, allotted to five named individuals.
- The location of the orchard, relative to an adjoining canal, adjoining fields, and an adjoining building is clearly indicated in the field plan (similarly only in the case of 6N-T777 in Zettler 1989).
- The presence of some legal clauses on the lower edge of the reverse shows that YBC 3879 is a juridical document. The document is dated to a specific year in the reign of King Amar-Suen of Ur.
§1.6. The required division of the irregularly shaped orchard into five parallel stripes of equal area leads to what is, essentially, a series of metric algebra problems of the second degree (quadratic equations). The given solutions to this series of metric algebra problems are (with one exception) fairly exact.
§1.7. All these unique features show that YBC 3879 provides an important piece of socio- economic history, at the same time as it is extraordinarily important from the point of view of history of mathematics, since it is one of the first documented appearances of metric algebra problems in a pre-Babylonian text. In addition, it may be the first documented appearance of metric algebra problems in a non-mathematical cuneiform text.
§2. Reconstructions of lost length and area numbers in the field plan on YBC 3879
Any detailed study of an Ur III field plan presupposes an adequate acquaintance with the system of sexagesimal counting numbers with or without place value notation and with the Ur III systems of length and area measures. A simple way of presenting those systems of measures is by way of their “factor diagrams”. The idea of using factor diagrams for a simple visualization of various Mesopotamian systems of measures was developed by the present author (see Friberg 2007b: app. 4).
§2.1.1. The factor diagram for sexagesimal numbers in place value notation (Spv) is simple, demonstrating that only two cuneiform number signs are used for sexagesimal numbers in place value notation, one for the “tens,” and another for the “ones” (figure 1a). It also shows that each ten is ten times bigger than the corresponding one, and that each one is 6 times bigger than the preceding, smaller ten.

Figure 1b: Factor diagram for Ur III length numbers.
§2.1.2. Equally simple is the factor diagram for the Ur III system of length numbers (L) (figure 1b), showing that the length unit with the Sumerian name ninda and the Akkadian name nindanum, to be understood as a measuring “pole,” is about 6 meters, and that the ninda is 12 times as big as the length unit kuš3 (Akk.: ammatum) “cubit.” It also shows that the “cubit” is 30 times as big as the šu-si (Akk.: ubānum) “finger.”
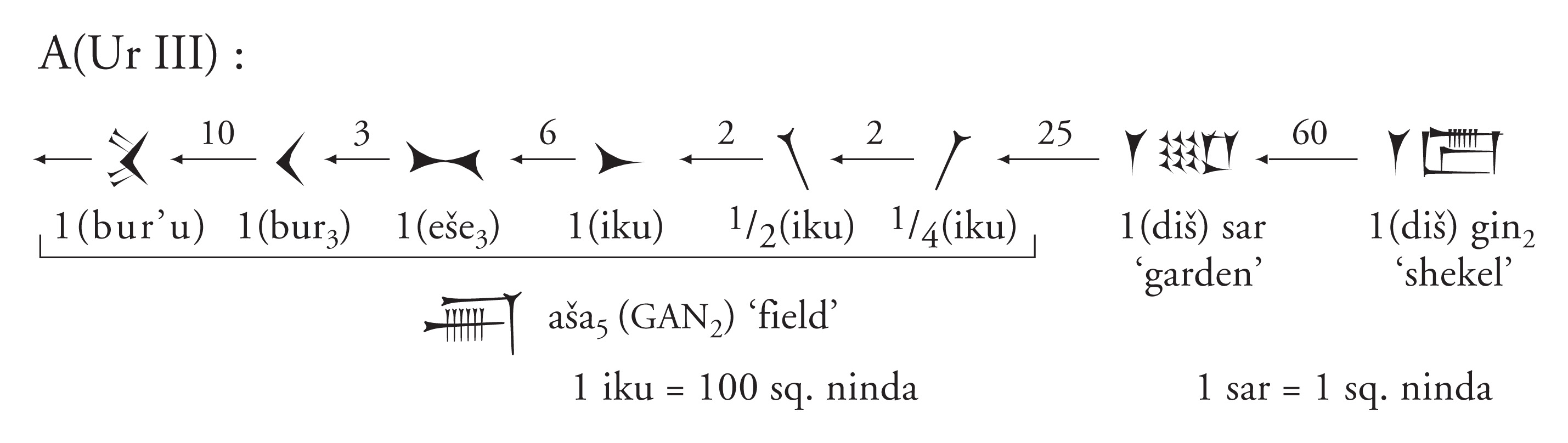
Figure 1c: Factor diagram for Ur III area numbers.
§2.1.3. The factor diagram for the Ur III system of area measures (A) is more complicated (figure 1c). It shows that there are special cuneiform number signs for the Ur III units of area measure bur’u, bur3, eše3, iku, as well as for 1/2 iku and 1/4 iku, but that the small units sar (square ninda) and gin2 “shekel” are counted with sexagesimal numbers. The diagram also shows that 1 bur’u = 10 bur3, 1 bur3 = 3 eše3, 1 eše3 = 6 iku, and 1 iku = 100 sar, while 1 sar = 60 gin2.
§2.2. After this necessary detour, it is now time to take a closer look at YBC 3879, beginning with the field plan on the reverse. The field plan shows a nearly square field, apparently a “temen” of the same kind as, but simpler than, the temens in MS 1984 (Friberg 2007b: figures 5.1-5.2), Ist O 1107 (op.cit. : figures 5.5-5.7), and Wengler 36 (Nissen, Damerow, and Englund 1993: figure 58). A temen is a regularly shaped field, typically made up of one or several rectangles or trapezoids. The usual meaning of the Sumerian word temen (Akk.: temēnum) is “foundation footprint.” In connection with a field plan, the word appears to refer to the initial form of a field, before various modifications. In the field plan on the reverse of YBC 3879, six fields of various shapes (three triangles and three (quasi-) trapezoids) have been removed from the temen, leaving as residue an irregularly shaped field.
§2.3. The lengths and names of the four sides of the temen are recorded along the sides of the temen. They are (with n. and c. as abbreviations for “ninda” and “cubit”):
| 16 n. | a2 i7-dba-ba6-ḫe2-gal2 | (north) |
| next to the canal Baba-ḫegal | ||
| 16 n. | a2 a-ša3 lu2-dutu a-zu | (east) |
| next to the field of Lu-Utu, the doctor | ||
| 14 n. 4 c. | [a2 e2 dšakan2-ba-ni] | (south) |
| [next to the house of Šakkan-bani] | ||
| 16 n. | a2 a-ša3 šuš3-ne | (west) |
| next to the field of the cattle managers |
Hence, the temen is a trapezoidal field, with the south side shorter than the north side.
§2.4. The canal Baba-ḫegal next to the north side of the temen is a known canal, dug by Ur-Baba, the predecessor of Gudea, governor of Lagash-Girsu, as commemorated in the year formula for the third year of his reign. This means that the date-grove figuring in this text was located somewhere in the Lagash-Girsu region.
§2.5. The lower right corner and part of the upper right corner of the field plan are so dam aged that eight recorded length numbers and three recorded area numbers are lost or unclear. Here follows a first attempt to reconstruct some of the lost length and area numbers.
§2.5.1. The four sides of the temen seem to be divided as follows:
| <14 n.> + 2 n. | = 16 n. | (north) |
| 10 1/2 n. + 2 n. + 3 [1/2 n.] | = 16 n. | (east) |
| 3 n. + 10 1/2 n. + [1/2 n. 4 c.] | = 14 n. 4 c. | (south) |
| [10 n.] + 6 n. | = 16 n. | (west) |
Therefore, three of the lost length numbers (those within straight brackets), and one unrecorded length number (within angular brackets), can be reconstructed without difficulty.
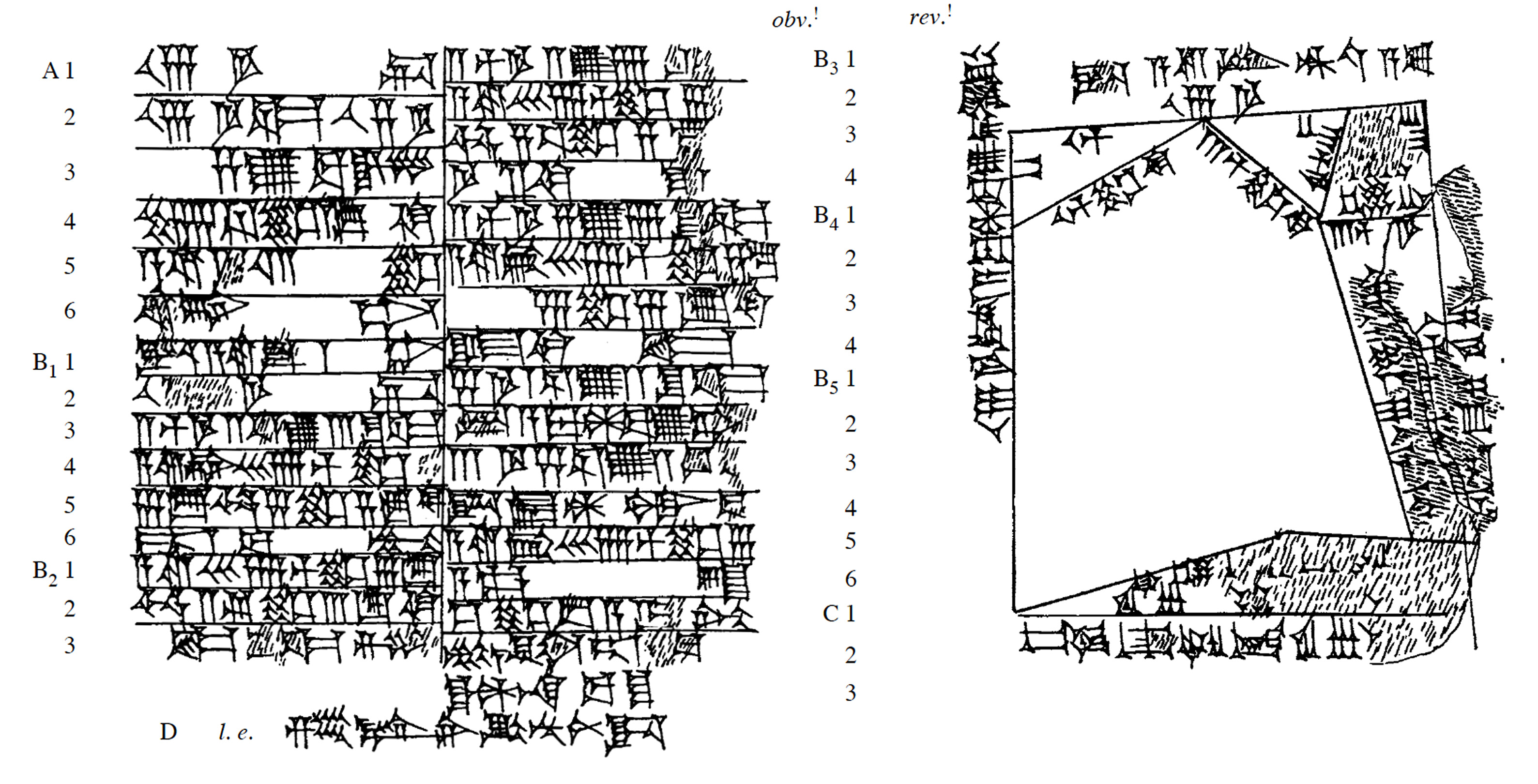

Figure 2: YOS 1, 24 = YBC 3879, obverse and reverse. Hand copy: A. T. Clay; photograph courtesy of the Yale Babylonian Collection.
§2.5.2. The areas of the six removed sections of the temen (called ki “rough ground”) are
| the triangular area | K1 = 1/2 · 10 1/2 n. · 2 n. = | 10 1/2 sar |
| the triangular area | K2 = (appr.) 1/2 · 2 n. · 3 1/2 n. = | 3 1/2 sar |
| the quadrilateral area | K3 = (appr.) (3 [1/2] n. + [4 n.]?)/2 · (3 1/2 n. + 3 n.)/2 = |
(appr.) 12 sar [11 gin2]? |
| the trapezoidal area | K4 = 10 1/2 n. · ([3 n.]? + [2 1/3 c.]?)/2 = | [1]6 [2/3 sar] 6 [2/3 gin2] |
| the trapezoidal area | K5 = 10 n. · ([1/2 n. 4 c.] + [4 c.])/2 = | [5 2/3 sar 10 gin2] |
| the triangular area | K6 = 1/2 · 6 n. · [4 c.] = | 1 sar |
Note the use of the approximate “false area rules” for the computation of the triangular area K2 and the quadrilateral area K4. The occasional use of approximate area rules in both mathematical and non-mathematical cuneiform texts is well known. See the discussion of the “surveyors’ formula” in Høyrup 2002: 229-231.
§2.5.3. These equations for the areas of the removed sections allow the reconstruction of two more of the lost or damaged length numbers in the field map, and of two of the lost or dam aged area numbers. Indeed, the equation for the removed area K6 shows that the lost length number for one side of the corresponding removed triangle must be [4 cubits]. If this reconstructed value is used in the equation for the removed area K5, it follows that the lost area number must be [5 2/3 sar 10 gin2].
§2.5.4. Another damaged area number, that of the trapezoidal area K4, can be reconstructed as follows: In the fourth line of the summary on the obverse, the recorded sum of the removed areas is K = 49 2/3 sar 1 gin2. Since K1 + K2 + K3 + K5 + K6
| = 10 1/2 sar + 3 1/2 sar +12 sar [11 gin2] | |
| + [5 2/3 sar 10 gin2] + 1 sar | |
| = 33 sar 1 gin2, | |
it follows that
| K4 = K - (K1 + K2 + K3 + K5 + K6) | |
| = 49 2/3 sar 1 gin2 - 32 sar 1 gin2 | |
| = 16 2/3 sar. | |
Note that this result does not completely agree with the value indicated on Clay’s hand copy (figure 2 above). More about this below.
§2.5.5. So far, the attempt to reconstruct the lost or damaged length and area numbers has been amazingly successful. Thus, consideration of how the sides of the temen are divided yielded the unambiguously reconstructed length numbers <14 n.> along the north side, 3 [1/2] n. along the east side, [1/2 n. 4 c.] along the south side, and [10 n.] along the west side. Consideration of the removed sections yielded the unambiguously reconstructed values [4 c.] in the case of K6, [5 2/3 sar 10 gin2] in the case of K5, and [16 2/3 sar] in the case of K4. This means that 5 out of 8 of the lost or damaged length numbers, and 2 out of 3 of the lost or damaged area numbers have been unambiguously reconstructed.
§2.5.6. However, at this point, the reconstruction attempt runs into considerable difficulties. First, according to Clay’s hand copy, the area of K4,which was reconstructed above with departure from the recorded sum of all removed areas (K = 49 2/3 sar 1 gin2), appears to be 16 ˹2/3˺ sar 6 ˹2/3˺ gin2 rather than the reconstructed value [16 2/3 sar]. Let us assume, for the sake of simplicity, that Clay’s value K4 = 16 ˹2/3˺ sar 6 ˹2/3 gin2˺ is correct, which means that the author of YBC 3879 made a small error when he computed the value of K.
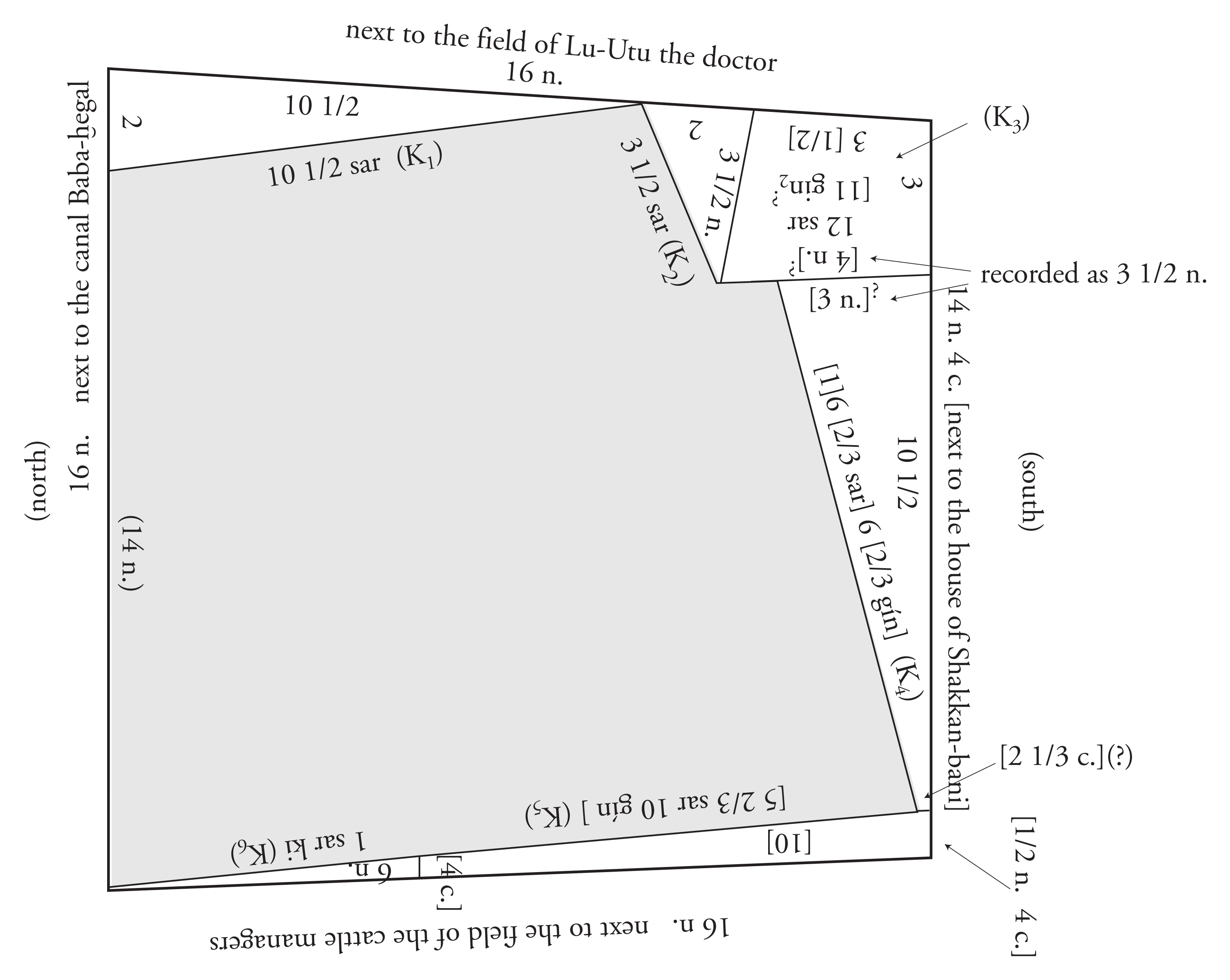
Figure 3: The field plan on YOS 1, 24 = YBC 3879, with corrections and reconstructions.
§2.5.7. Next, the removed quadrilateral in the upper right corner of the temen cannot have three sides of length 3 1/2 n. and one side of length 3 n., as indicated in Clay’s hand copy, because then the usual false area rule would give the following value for the area K3:
| (3 1/2 n. + 3 1/2 n.)/2 · (3 1/2 n. + 3 n.)/2 |
| = 3 1/2 n. · 3 n. 3 c. |
| = 11 sar 22 1/2 gin2, |
a result that does not agree with the recorded area number for K3. Besides, the field plan clearly indicates that the lower side of the trapezoid is longer than the upper side. The simplest way out of this dilemma is to assume, somewhat arbitrarily, that the lower side of the removed trapezoid K3 should be [4 n.], and that the corresponding area should be
| (4 n. + 3 1/2 n.)/2 · (3 1/2 n. + 3 n.)/2 |
| = 3 1/2 n. 3 c. · 3 n. 3 c. |
| = (appr.) 12 sar [11 gin2]. |
§2.5.8. Another inconsistency in the text is that the removed trapezoidal field K4 along the right edge of the temen cannot have its upper side equal to 3 1/2 ninda, as recorded in the field plan, according to Clay’s hand copy. Indeed, if the length of the trapezoid is 10 1/2 n. and the area is [1]6 [2/3 sar] 6 [2/3 gin2], then the sum of the two parallel sides must be
| 2 · 16 2/3 sar 6 2/3 gin2 / 10 1/2 n. |
| = (appr.) 3 n. 2 1/3 c. |
The simplest way out of this difficulty is to assume that the author of the text made another mistake, and that the two parallel sides of the trapezoid K4 should be [3 n.] and [2 1/3 c.], respectively, as indicated in figure 3. This means, in particular, that the lower side of the trapezoid K3 and the upper side of the trapezoid K4 cannot coincide, as they seem to do in the field plan! Maybe the field plan on YBC 3879 is a somewhat erroneous copy of an original field plan on a clay tablet with a damaged upper right corner? Note, by the way, that the field plan is not very accurately drawn and partly out of scale. That is a frequently occurring phenomenon in other known field plan texts. See, for instance, figure 17 below.
§2.6. The summary and the field division on the obverse
§2.6.1. In lines A 1-3 on the obverse of YBC 3879 (see the transliteration below), the lengths of the sides of the trapezoidal temen are given as
16 ninda uš, 16 ninda sag, 14 ninda 4 kuš3 ba-gi4.
The use of the term uš “length,” “flank” for the “long sides” and the term sag “front” for one of the “short sides” of the trapezoid is typical for “southern” field texts in third millennium Mesopotamia (Liverani 1996: 19). It is also the terminology used in Old Babylonian mathematical texts. The term ba-gi4 in line A 3, meaning something like “brought back, reduced,” indicates that the south side of the trapezoid is shorter than the north side. The term is known to appear in the form ba-an-gi4 and with a similar meaning in the brick wall text AO 7667 from Ur III Umma (see Friberg 2001: 136; see also Robson 1999: 149, fn. 38, and Heimpel 2004). In AO 7667, the phrase
1/2 ninda dagal 1 kuš3 ba-an-gi4 4 kuš3 sukud
in paragraph a7.2 of the text, for instance, refers to a brick wall 1/2 ninda = 6 cubits wide at the base, but only 1 cubit wide at the top, and 4 cubits high.
§2.6.2. Transliteration and translation of YOS 1, 24 = YBC 3879, obv.
| A | 1 | 16 ninda uš | 16 ninda length | length |
| 2 | 16 ninda sag | 16 ninda front | front | |
| 3 | 14 ninda 4 kuš3 ba-gi4 | 14 ninda 4 cubits reduced | reduced | |
| 4 | 49 2/3 sar 1 gin2 ki | 49 2/3 sar 1 gin2 rough ground | K | |
| 5 | a-ša3 ˹3(geš2)˺ 13 sar | field: 3 (· 60) 13 sar | A = T-K | |
| 6 | ša3-bi-ta | out of which | ||
| B1 | 1 | a2 a-ša3 kuš7-bi! | next to the field of donkey-herdsmen | west side |
| 2 | ˹16˺ ninda uš | 16 ninda length | length | |
| 3 | 2 1/2 ninda 2 ˹2/3˺ kuš3 3 šu(-si) sag | 2 1/2 ninda 2 2/3 cubits 3 fingers front | s1 | |
| 4,5 | a-ša3-bi 38 1/2 sar 6 gin2 sag10 | its field 38 1/2 sar 6 gin2 good | A/5 | |
| 5 sar 4 gin2 ki | 5 sar 4 gin2 rough ground | K1* | ||
| 6 | ab-ba-mu | Abbamu | PN1 | |
| B2 | <2 1/2 ninda 1 kuš3 sag> | <2 1/2 ninda 1 cubit front> | s2 | |
| 1,2 | a-ša3 38 1/2 sar 6 gin2 sag10 | field 38 1/2 sar 6 gin2 good | A/5 | |
| 2 2/3 sar 3 gin2 ki | 2 2/3 sar 3 gin2 rough ground | K2* | ||
| 3 | inim-x-du11-ge | Inim-x-duge | PN2 | |
| B3 | 1 | 2 1/2 ninda 2 kuš3 8 šu(-si) ˹sag˺ | 2 1/2 ninda 2 cubits 8 fingers front | s3 |
| 2,3 | a-ša3 38 1/2 sar 6 ˹gin2˺ sag10 | field 38 1/2 sar 6 gin2 good | A/5 | |
| 4 1/3 sar 4 ˹gin2˺ [ki] | 4 1/3 sar 4 gin2 rough ground | K3* | ||
| 4 | nig2-si-sa2-e | Nig-sisae | PN3 | |
| B4 | 1 | 2 1/2 ninda 4 kuš3 8 šu(-si) sag | 2 1/2 ninda 4 cubits 8 fingers front | s4 |
| 2 | a-ša3-bi 38 1/2 sar 4 gin2 sag10 | its field 38 1/2 sar 6! gin2 good | A/5 | |
| 3 | 7 sar 6 gin2 ki | 7 sar 6 gin2 rough ground | K4* | |
| 4 | nimgir-sa2-du11 | Nimgir-sadu | PN4 | |
| B5 | 1 | 5 ninda 1 2/3 kuš3 2 šu(-si) sag | 5 ninda 1 2/3 cubits 2 fingers front | s5' |
| 2 | a2 i2-dba-ba6-ḫe2-[gal2] | next to the canal Baba-ḫegal | north side | |
| 3 | 3 ninda 5 2/3 kuš3 2 ˹šu(-si)˺ [sag] | 3 ninda 5 2/3 cubits 2 fingers front | s5" | |
| 4 | a2 e2 dšakan2-ba-[ni] | next to the house of Šakkan-bani | south side | |
| 5 | a-ša3-bi 38 1/2 sar < 6 gin2 sag10> | its field 38 1/2 sar 6 < gin2, |
A/5 | |
| <30 1/3 sar 4 gin2 ki> | <30 1/3 sar 4 gin2 rough ground> | K5* | ||
| 6 | a-kal-la | Akalla | PN5 | |
| C | 1 | geškiri6 ba-a-ur-gu-ba | the orchard Baya-Urguba | |
| 2,3 | mu en-unu6-gal-an-na ba-ḫun | the year En-unugal-anna was installed | AS 5 | |
| D | 1 | zi lugal i3-gal2 nu kur2-da | the “by the royal life” is here not to be altered | legal clauses |
§2.6.3. In lines A 4-5 of the obverse, the statement
49 2/3 sar 1 gin2 ki / a-ša3 [3(geš2)] 13 sar (geš2 = 60)
means that the sum K of the areas of the removed parts (ki) of the temen is 49 2/3 sar 1 gin2 (should be 7 2/3 gin2), and that the remaining area T - K is 3(60) 13 sar. The (corrected) computation of the sum of the areas of the removed sections was explained above. The computation of the area of the remaining part of the temen is easy:
| T = (appr.) 16 ninda · (16 ninda + 14 ninda 4 cubits)/2 | |
| = 16 ninda · 15 ninda 2 cubits = 4(60) 2 2/3 sar. | |
| A = T - K = 4(60) 2 2/3 sar - 49 2/3 sar (1 gin2) | |
| = 3(60) 13 sar. | |
The term in line A 6,
ša3-bi-ta “out of which” (lit. “from its interior”)
indicates that the totally available field, of area A = T - K, is to be divided into a number of sub-fields. The term is well known from Sumerian administrative texts.
§2.6.4. Although that is neither explicitly stated nor shown in the field map, it is clear that the totally available field is to be divided into five pieces, all of the same area, namely
A/5 = 3(60) 13 sar / 5 = 38 1/2 sar 6 gin2
True enough, this value is recorded five times in the text on the obverse of YBC 3879, in lines B1 4-5, B2 1-2, B3 2-3, B4 2 (corrected here), and B5 5. In each one of the five cases, such a fifth of the available area is called “good” land (sag10).
§2.6.5. The way in which the irregularly formed field with the area A = 3(60) 13 sar is divided into five pieces of equal area is indicated only implicitly in the text on the obverse, through the listing in paragraphs B1-B5 of the following five partial fronts (sag):
| s1 | = 2 1/2 ninda 2 [2/3] cubits 3 fingers | line B1 3 | |
| s2 | = <2 1/2 ninda 1 cubit> | ——— | |
| s3 | = 2 1/2 ninda 2 cubits | line B3 1 | |
| s4 | = 2 1/2 ninda 4 cubits 8 fingers | line B4 1 | |
| s5' | = 5 ninda 1 2/3 cubits 2 fingers | next to the canal Baba-hegal | line B5 1 |
| s5" | = 3 ninda 5 2/3 cubits 2 fingers | next to the house of Shakkan-bani | line B5 3 |
It will be shown below how the missing value for the partial front s2 can be reconstructed. The reconstructed value is inserted in the second line above, between angular brackets.
§2.6.6. Also listed in paragraphs B1-B5 are four areas of removed sections of land (ki):
| K1* | = 5 sar 4 gin2 | line B1 5 |
| K2* | = 2 2/3 sar 3 gin2 | line B2 2 |
| K3* | = 4 1/3 sar 4 gin2 | line B3 3 |
| K4* | = 7 sar 6 gin2 | line B4 3 |
| K5* | = (30 1/3 sar 4 gin2) | ——— |
The fifth of these areas is not mentioned in the text, but it is easy to reconstruct the missing value K5*, since the total area of all removed sections of land is known (line A 4).
§2.6.7. The division of the totally available “good” land into five pieces of equal area is, apparently, accomplished in an interesting fashion. In similarity with the case of Ist O 1107 and Wengler 36, two significant field plans from Umma discussed in Friberg 2007b: ch. 5 (see, in particular, figure 5.6 there, based on an idea first proposed by Quillien 2003), it is arbitrarily assumed that the trapezoidal temen in the case of YBC 3879 can be divided into a series of parallel stripes, beginning with a series of rectangles, and ending with a trapezoid. In this way, the problem how to divide the “good” land into five pieces of equal area is reduced to the problem of finding the corresponding fronts of four rectangles (s1-s4) and of the final trapezoid (s5' and s5"). The situation is illustrated in figure 4 below.
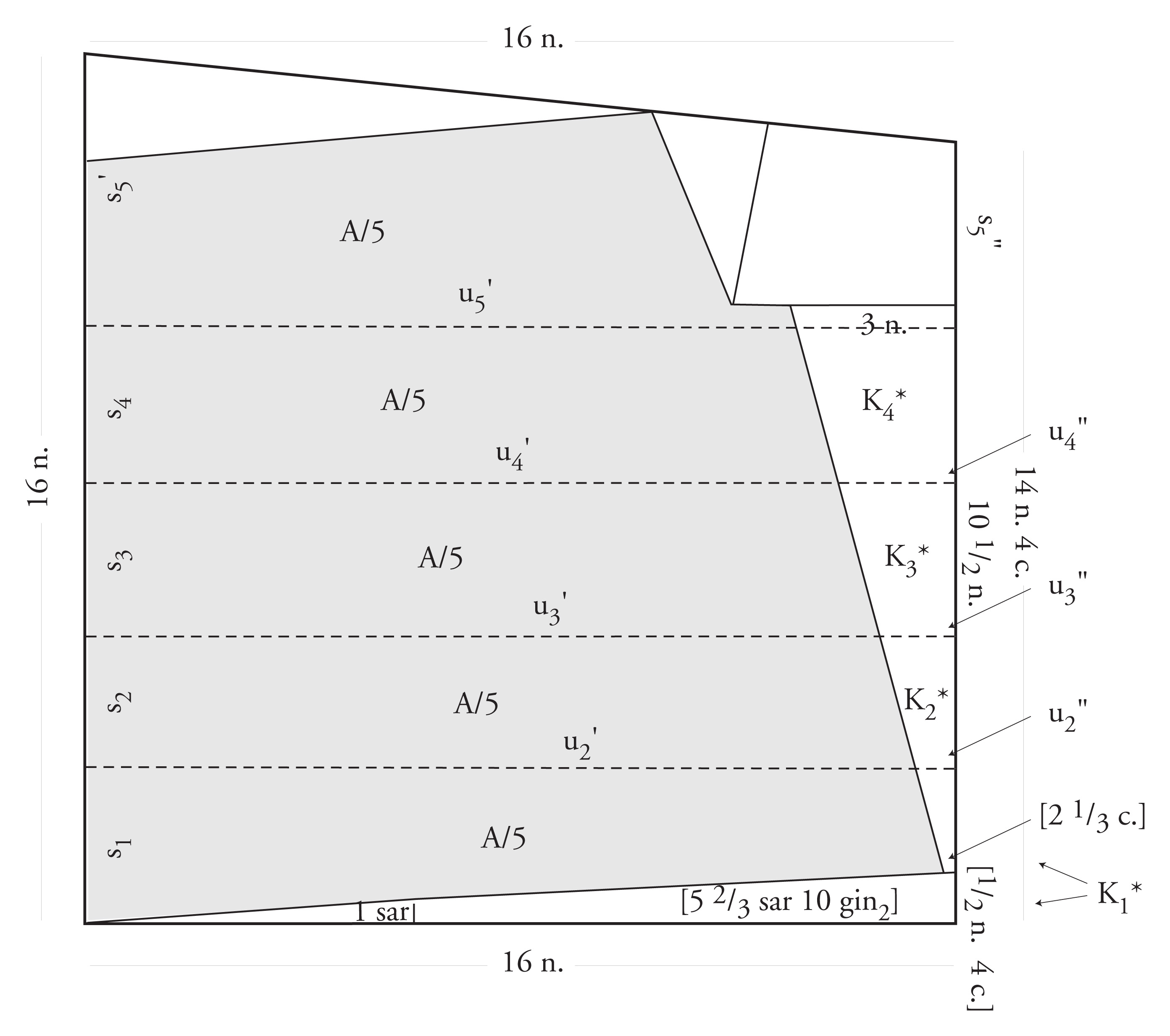
Figure 4: The division of the temen in YBC 3879 into four rectangles and a trapezoid.
§2.6.8. The legal clauses on the lower edge (paragraph D) can be read as
The “by the royal life” is here. It must not be altered.
The phrase “by the royal life” alludes to the common legal practice of swearing oaths invoking the reigning king by name. What “must not be altered” is the outcome of the legal process in which the oath was sworn. The presence of these legal clauses on the tablet's edge and the subscription of the date implies that the tablet is a juridical document recording the legal division of an orchard among five named individuals, who have accepted the division on oath.
§3. The algorithmic procedure for the computation of the fronts of the stripes
§3.1. The computation of the first partial front (s1) must, conceivably, have proceeded as follows. The value of s1 has to be chosen so that the area of the first stripe (16 n. · s1) minus A/5 (38 1/2 sar 6 gin2) is equal to the combined area K1* of those parts of the removed fields (ki “rough ground”) which fall within the first stripe. This combined area is the sum of the areas of the removed fields at the west side of the temen (1 sar + 5 2/3 sar 10 gin2 = 6 2/3 sar 10 gin2) and the area of the part of the removed trapezoid at the south side of the temen which falls within the first stripe.
§3.1.1. Now, according to the suggested reconstruction in figure 3, this trapezoid has the length 10 1/2 ninda and the parallel fronts 3 ninda and 2 1/3 cubits. In a similar situation in an Old Babylonian mathematical text, the “feed” f of the trapezoid (essentially, the inclination of its side) would be given as (with n. = ninda, c. = cubit):
f = (3 n. - 2 1/3 c.) / 10 1/2 n. = 2 1/2 n. 3 2/3 c. / 10 1/2 n.
In terms of sexagesimal numbers in place value notation:
f = 2;48 20 n. / 10;30 n. = 2;48 20 / 10;30.
§3.1.2. However, 10;30 is not a regular sexagesimal number, which means that there is no exact reciprocal to 10:30. Without any reciprocal available, the division can be carried out in the following way, for instance:
f = 2;48 20 / 10;30 = (appr.) 2 / 10 = ;12, ;12 · 10;30 = 2;06, deficit: 2;48 20 - 2;06 = ;42 20.
;42 20 / 10;30 = (appr.) ;40 / 10 = ; 04, ;04 · 10;30 = ;42, deficit ;00 20.
Hence, approximately,
f = ;12 + ;04 = ;16.
§3.1.3. Without the use of sexagesimal numbers in place value notation, the computation of the feed f can be carried out instead in the following way, for instance (with f. = finger):
f = 2 1/2 n. 3 2/3 c. / 10 1/2 n. = (appr.) 1/5, 1/5 · 10 1/2 n. = 2 n. 1 c. 6 f.,
deficit: 1/2 n. 2 1/3 c. 4 f.
1/2 n. 2 1/3 c. 4 f. / 2 n. 1 c. 6 f. = (appr.) 1/2 n. 2 c. / 2 n. = 8 c. / 24 c. = 1/3,
1/3 · 2 n. 1 c. 6 f. = 1/2 n. 2 1/3 c. 2 f., deficit: 2 f.
Hence, approximately,
f = 1/5 + 1/3 · 1/5.
(Note that this kind of fraction, which is known from both Old and Late Babylonian texts, may occur also in the Sargonic [Old Akkadian] mathematical text ZA 94, 3, lines 3-5. See Friberg 2009 in a commentary to Robson 2008: p. 80; see also Friberg 2005: §2.2.7.)
§3.1.4. In a similar fashion, it can be shown that the inverse “feed” (1/f) is, approximately, with and without sexagesimal place value notation, respectively,
1/f = 3;45 or 1/f = 3 2/3 1/8 · 2/3.
When these values for the “feed” and its inverse are known, the first partial front s1 can be computed in the following way.
§3.1.4.1. The first step is to compute the length
u1' = 16 n. - 2 1/3 c. = 15 1/2 n. 3 2/3 c.
(see the diagram in figure 5), and the area
B = A/5 - (16 n. · 1/2 n. 4 c. - 6 2/3 sar 10 gin2) = 38 1/2 sar 6 gin2 - 6 1/2 sar = 32 sar 6 gin2
For the next step, it is convenient to count with the new unknown
a = s1 - 1/2 n. 4 c.
(see again the diagram in figure 5). Then it is easy to see that the area B that was computed above is also equal to the area of the rectangle with the sides a and u1' minus the area of the right triangle with the sides a and b = f · a. In quasi-modern notations,
u1' · a - f/2 · sq. a = B where u1' = 15 1/2 n. 3 2/3 c., f = 1/5 + 1/3 · 1/5, and B = 32 sar 6 gin2
In other words, the value of a = s1 - 1/2 n. 4 c. can be computed as the solution to a quadratic equation with known coefficients.

Figure 5: A quadratic equation for a = s1 – 1/2 n. 4 c, where s1 is the first partial front.
§3.1.4.2. Now, if both sides of this quadratic equation for a are multiplied by 2 f, the result is the following quadratic equation for the new unknown b = f · a:
2 · u1' · b - sq. b = f · 2 B.
Now, let (as in figure 5)
u2' = u1' - b.
Then the equation above for b can, in its turn, be reduced to a quadratic equation for u2':
sq. u2' = sq. u1' - f · 2 B.
See the explanation in §5 below.
§3.1.4.3. Now (with n. = ninda, c. = cubit, f. = finger),
| f · 2 B = 1/5 1/3 · 1/5 · 2 · 32 sar 6 gin2 |
| = 1/5 1/3 · 1/5 · 1(60) 4 sar 12 gin2 |
| = (appr.) 12 5/6 sar 1/3 gin2 + 4 sar 16 2/3 gin2 |
| = 17 sar 7 gin2, |
and
sq. 15 1/2 n. 3 2/3 c. = (appr.) 4(60) 9 2/3 sar 9 gin2.
Consequently,
sq. u2' = (appr.) 4(60) 9 2/3 sar 9 gin2 - 17 sar 7 gin2 = 3(60) 52 2/3 sar 2 gin2.
§3.1.4.4. Computing the square sides (square roots) of both sides of this equation (by use of some appropriate method for successive approximations of square roots; see, for instance, Friberg 1997: §8), one finds that
u1' - b = u2' = sqs. 3(60) 52 2/3 sar 2 gin2 = (appr.) 15 n. 3 c. 2 f.
(See again figure 5) This means that the value of b = f · a is
b = u1' - u2' = 15 1/2 n. 3 2/3 c. - 15 n. 3 c. 2 f. = 1/2 n. 1/2 c. 3 f.
Consequently,
a = 1/f · b = (3 2/3 1/8 · 2/3) · 1/2 n. 1/2 c. 3 f. = (appr.) 2 n. 2/3 c. 3 f.
and
s1 = a + 1/2 n. 4 c. = 2 1/2 n. 4 2/3 c. 3 f.
§3.1.4.5. Given in the text is the value
| s1 = 2 1/2 n. 2 2/3 c. 3 f. | line B1 3 |
| corresponding to the incorrect value a = 1 1/2 n. 4 2/3 c. 3 f. | |
The difference between the value for s1 given in the text and the value computed above is precisely 2 cubits. The difference may be due to a simple reading error, 2 instead of 4. The Ur III forms of the number signs for 2 (a pair of upright wedges) and 4 (a pair of upright wedges atop another pair of upright wedges) are easily mistaken for one another.
§3.1.4.6. Once the value of the first partial front s1 has been found, the corresponding value of K1* can be computed, without trouble, as follows:
If
| s1 = 2 1/2 n. 2 2/3 c. 3 f., |
the incorrect value given in the text, then
| K1* = 16 n. · s1 - A/5 = (appr.) 43 1/2 sar 10 gin2 - 38 1/2 sar 6 gin2 | line B1 5 | |
| = 5 sar 4 gin2 |

Figure 6: A quadratic equation for the second partial front s2.
§3.2. In paragraph B2 of the text on the obverse, the > value of the second partial front s2 is missing, probably by mistake. The value can be reconstructed straightaway, since
16 n. · s2 - A/5 = K2*, where K2* = 2 2/3 sar 3 gin2 (line B2 2),
so that, counting backwards,
s2 = (A/5 + K2*)/16 n. = (38 1/2 sar 6 gin2 + 2 2/3 sar 3 gin2)/16 n. = (41 sar 19 gin2)/16 n. = (appr.) 2 1/2 n. 1 c.
§3.2.1. Although the original author of YBC 3879, or someone after him, forgot to record the result on the tablet, the value of s2 may have been computed in the following way. The incorrect value of the length u2" = 2 1/3 c. + f · a (see figures 5 and 6) corresponding to the incorrect value of s1 given in the text is
u2" = 2 1/3 c + f · a = 2 1/3 c. + 1/5 1/3 · 1/5 · 1 1/2 n. 4 2/3 c. 3 f. = (appr.) 2 1/3 c. + 1/2 n. 2 f. = 1/2 n. 2 1/3 c. 2 f.
§3.2.2. With the corresponding incorrect value
u2' = 16 n. - u2" = 16 n. - 1/2 n. 2 1/3 c. 2 f. = 15 n. 3 1/2 c. 3 f.
(see again figure 6), the value of s2 is the solution to the quadratic equation
u2' · s2 - f /2 · sq. s2 = A/5 = 38 1/2 sar 6 gin2
§3.2.3. As before, if both sides of this equation are multiplied by 2 f, the result is that
2 u2' · b2 - sq. b2 = f · 2 A/5, where b2 = f · s2.
This equation, in its turn, can be reduced to (see §5.2.4 below)
sq. (u2' - b2) = sq. u2' - f · 2 A/5 = sq. 15 n. 3 1/2 c. 3 f. - 1/5 1/3·1/5 · 2 · 38 1/2 sar 6 gin2
= (appr.) 3(60) 54 sar 5 gin2 - 20 1/2 sar 5 gin2 = 3(60) 33 1/2 sar.
§3.2.4. Computing the square sides (square roots) of both sides of this equation, one finds that
u3' = u2' - b2 = sqs. 3(60) 33 1/2 sar = (appr.) 14 1/2 n. 1 1/3 c.
Consequently,
b2 = u2' - u3' = 15 n. 3 1/2 c. 3 f. - 14 1/2 n. 1 1/3 c. = 1/2 n. 2 c. 8 f.
§3.2.5. Then, finally,
s2 = 1/f · b2 = 3 2/3 1/8 · 2/3 · 1/2 n. 2 c. 8 f. = (appr.) 2 1/2 n. 1 c.
This is precisely the easily reconstructed value which is missing in the text, and which leads to the following value for the removed section K2*:
K2* = 16 · s2 - A/5 = 41 sar 20 gin2 - 38 1/2 sar 6 gin2 = 2 2/3 sar 4 gin2
The value recorded in the text is, for some reason, 1 gin2 smaller, a trivial mistake:
K2* = 2 2/3 sar 3 gin2 line B2 3
§3.2.6. The computation of the third partial front s3 proceeds in precisely the same way. It starts with the computation of
u3" = u2" + f · s2 = 1/2 n. 2 1/3 c. 2 f. + 1/5 1/3 · 1/5 · 2 1/2 n. 1 c. = 1/2 n. 2 1/3 c. 2 f. + 1/2 n. 2 c. 8 f. = 1 n. 4 2/3 c.
Then the value of s3 can be computed as the solution to the quadratic equation
u3' · s3 - f /2 · sq. s3 = A/5,
where u3' = 16 n. - u3" = 14 1/2 n. 1 1/3 c. and A/5 = 38 1/2 sar 6 gin2
Therefore, in the same way as before,
sq. (u3' - b3) = sq. u3' - f · 2 A/5 = sq. 14 1/2 n. 1 1/3 c. - 1/5 1/3 · 1/5 · 2 · 38 1/2 sar 6 gin2
= (appr.) 3(60) 33 1/3 sar 9 gin2 - 20 1/2 sar 5 gin2 = 3(60) 12 2/3 sar 14 gin2
§3.2.7. Computing the square sides (square roots) of both sides of this equation, one finds that
u4' = u3' - b3 = sqs. 3(60) 12 2/3 sar 14 gin2 = (appr.) 13 1/2 n. 4 2/3 c.
Consequently,
b3 = u3' - u4' = 14 1/2 n. 1 1/3 c. - 13 1/2 n. 4 2/3 c. = 1/2 n. 2 2/3 c.
Therefore, finally,
s3 = 1/f · b3 = 3 2/3 1/8 · 2/3 · 1/2 n. 2 2/3 c. = (appr.) 2 1/2 n. 2 1/2 c.
The value of s3 recorded in the text is
| s3 = 2 1/2 n. 2 c. 8 f., | line B3 1 |
which is 7 fingers smaller. Accordingly, the value of K3* can be computed as follows
| If | s3 = 2 1/2 n. 2 1/2 c. 8 f. (as in the text), then | |
| K3* = 16 n. · s3 - A/5 = (appr.) 43 sar - 38 1/2 sar 6 gin2 = 4 1/3 sar 4 gin2 | line B3 3 |
§3.2.8. The computation of the fourth partial front s4 begins with the computation of
u4" = u3" + f · s3 = 1 n. 4 2/3 c. + 1/5 1/3 · 1/5 · 2 1/2 n. 2 c. 8 f. (the value given in the text) = (appr.) 1 n. 4 2/3 c. + 1/2 n. 2 1/2 c. 3 f. = 2 n. 1 c. 8 f.
Then the value of s4 can be computed as the solution to the quadratic equation
u4' · s4 - f /2 · sq. s4 = A/5,
where
u4' = 16 n. - u4" = 13 1/2 n. 4 2/3 c. 2 f. and A/5 = 38 1/2 sar 6 gin2
Therefore, in the same way as in the preceding steps of the algorithm,
sq. (u4' - b4) = sq. u4' - f · 2 A/5 = sq. 13 1/2 n. 4 2/3 c. 2 f. - f · 2 · 38 1/2 sar 6 gin2
= (appr.) 3(60) 13 sar 3 gin2 - 20 1/2 sar 5 gin2 = 2(60) 52 1/3 sar 8 gin2
§3.2.9. Computing the square sides (square roots) of both sides of this equation, one finds that
u5' = u4' - b4 = sqs. 2(60) 52 1/3 sar 8 gin2 = (appr.) 13 n. 1 1/2 c. 3 f.
Consequently,
b4 = u4' - u5' = 13 1/2 n. 4 2/3 c 2 f. - 13 n. 1 1/2 c. 3 f. = 1/2 n. 3 c. 4 f.
Therefore, finally,
s4 = 1/f · b4 = 3 2/3 1/8·2/3 · 1/2 n. 3 c. 4 f. = 2 1/2 n. 4 c. 8 f.
The value of s4 recorded in the text is the same:
s4 = 2 1/2 n. 4 c. 8 f. line B4 1
§3.3.1. The sum of the lengths of the first four partial fronts (with the values recorded in the text, plus the securely reconstructed value of s2) is
s1 + s2 + s3 + s4
= 2 1/2 n. 2 2/3 c. 3 f. + 2 1/2 n. 1 c. + 2 1/2 n. 2 c. 8 f. + 2 1/2 n. 4 c. 8 f. = 10 1/2 n. 4 c. 9 f.
§3.3.2. Since the sum of all five partial fronts (along the north side) is 16 n., it follows that
s5' = 16 n. - 10 1/2 n. 4 c. 9 f. = 5 n. 1 2/3 c. 1 f.
(The value recorded in line B5 1 of the text is 1 finger larger, a negligible error.) It is equally simple to compute the fifth partial front along the south side, which should be
s5" = 14 n. 4 c. - 10 1/2 n. 4 c. 9 f. = 3 n. 5 2/3 c. 1 f.
(The value recorded in line B5 3 of the text is again 1 finger larger.)
§3.3.3. It is also simple to compute the total area K5* of the fields removed from the top trapezoid. Since
K1* + K2* + K3* + K4* = 5 sar 4 gin2 +2 2/3 sar 3 gin2
+ 4 1/3 sar 4 gin2 + 7 sar 6 gin2 = 19 sar 17 gin2,
while K = K1* + K2* + K3* + K4* + K5* = 49 2/3 sar 1 gin2,
it follows that
K5* = 49 2/3 sar 1 gin2 - 19 sar 17 gin2 = 30 1/3 sar 4 gin2
However, a value for K5* is missing in the text, probably by mistake.
§3.3.4. Of the values for the partial fronts computed above, s2 and s4 and are identical with the values recorded in the text, while s3, s5' and s5" differ from the recorded values with 7, 1, and 1 fingers, respectively, and s1 by precisely 2 cubits. The recorded value for s1 is probably due to a small mistake on the part of the author of the text (reading 2 instead of 4), and the small differences in the cases of s3, s5' and s5" may be due to the complexity of the necessary calculations, involving subtractions, multiplications, divisions, and computations of square sides (square roots). Note that this (relatively) successful explanation of the computation of the recorded values for the partial fronts strongly confirms the correctness of the reconstructed values in figure 3 of lost or damaged length and area numbers!
Note: The value of u2' is computed twice above, in two different ways, the first time as
u2' = u1' - b = (appr.) 15 n. 3 c. 2 f.,
and the second time as
u2' = 16 n. - u2" = (appr.) 15 n. 3 1/2 c. 3 f.
§3.3.5. The difference of 16 fingers between the two values for u2' is caused by the use of an erroneous value for s1 in the computation of u2". In spite of this difference, the computed value of s2 is the same as the value recorded in the text. In the case of u3', the two values computed in different ways are equal. However, in the case of u4', the two values computed in different ways differ by 2 fingers. The difference of 2 fingers between the two values is caused by the use of an erroneous value for s3 in the computation of u4". In spite of this difference, the computed value of s4 is the same as the value recorded in the text. It is, for these reasons, likely that the values recorded in the text were computed in precisely the way suggested on the preceding pages, including the computation twice of both u2' and u4'.
§4. On the use of sexagesimal numbers in place value notation in the Ur III period
§4.1.1. It was shown above how the needed computations may have been effected by the author of YBC 3879 in terms of non-positional sexagesimal numbers, and Ur III length and area numbers. Compare the online paper Friberg 2005, where it is shown that all computations in known mathematical cuneiform texts from the 3rd millennium BC, before the time of the Ur III period, can have been carried out without the use of sexagesimal numbers in place value notation.
§4.1.2. On the other hand, the computations of the partial fronts in YBC 3879 would have been considerably simplified if the author of the text had had recourse to sexagesimal numbers in place value notation. The calculated values of the partial fronts could then have been expressed as follows in terms of sexagesimal numbers in relative (or floating) place value notation without zeros, silently understood as multiples of the basic length unit ninda:
| s1 = | 2 1/2 n. 2 2/3 c. 3 f. = | 2 43 50 | should be 2 53 50 |
| s2 = | 2 1/2 n. 1 c. = | 2 35 | |
| s3 = | 2 1/2 n. 2 c. 8 f. = | 2 41 20 | should be 2 42 30 |
| s4 = | 2 1/2 n. 4 c. 8 f. = | 2 51 20 | |
| s5' = | 5 n. 1 2/3 c. 2 f. = | 5 08 40 | should be 5 08 30 |
| s5" = | 3 n. 5 2/3 c. 2 f. = | 3 28 40 | should be 3 28 30 |
§4.1.3. In terms of sexagesimal numbers in relative (floating) place value notation, the successive steps in the computation of, for instance, the fourth partial front s4 would have taken the following form (in conveniently quasi-modern notations):
f = 16, 1/f = 3 45,
u4" = u3" + f · s3 = 1 23 20 + 16 · 2 41 20 = (appr.) 1 23 20 + 43 = 2 06 20,
u4' = 16 n. - u4" = 16 - 2 06 20 = 13 53 40, 13 53 40 · s3 - 16 · sq. s3 = 38 36.
Hence,
2 · 13 53 40 · b4 - sq. b4 = 16 · 2 · 38 36,
sq. (13 53 40 - b4) = sq. 13 53 40 - 16 · 2 · 38 36 = (appr.) 3 13 03 - 20 35 = 2 52 28,
b4 = 13 53 40 - sqs. (2 52 28) = 13 53 40 - (appr.) 13 08 = 45 40.
Therefore, finally,
s4 = 1/f · b4 = 3 45 · 45 40 = 2 51 20.
This result has to be interpreted as
2;51 20 ninda = 2 1/2 ninda 4 cubits 8 fingers,
the value recorded in the text.
§4.1.4. It is, indeed, possible that the author of YBC 3879 made use of sexagesimal numbers in place value notation in his quite complex calculations. Such numbers are known to have been used in a few texts from the Ur III period, including the non-mathematical account of silver YBC 1793 = YOS 4, 293 (Keiser 1919; see Friberg 2005: §4 for a more detailed discussion of this interesting text; a photo of YBC 1793 can be found in Robson 2008: 79).
§4.1.5. In YOS 4, 293, the sum of the following numbers in sexagesimal place value notation
14 54, 29 56 50, 17 43 40, 30 53 20
is expressed in standard metrological notation as the weight number 1 1/2 mina 3 1/2 gin2 - 7 barleycorns of silver. In sexagesimal place value notation the sum would have been written as 1 33 27 40. Similarly, the sum of the six numbers
2 54, 45, 28, 17, 2 28, 27
is written as the weight number
7 minas 19 gin2 of silver,
while the sum in place value notation would have been written in the form 7 19.
§4.1.6. Incidentally, the silver account YOS 4, 293 = YBC 1793 and the juridical document YOS 1, 24 = YBC 3879 were both written in the same year, namely the fifth year of the reign of Amar-Suen, the third king of the neo-Sumerian Ur III dynasty. The year formula for that king, in its full form, is
Year: “En-unugal-anna was installed as en-priest of Inanna in Uruk.”
This year formula appears in YBC 1793 in the following abridged version:
Year: “en-priest of Inanna.”
It appears again in YBC 3879, but in another abridged version:
Year: “En-unugal-anna was installed.”
§4.2.1. There are a handful of known tables of reciprocals, which presumably are from the Ur III period and which do make use of sexagesimal numbers in place value notation, but which are quite unlike the tables of reciprocals of the Old Babylonian standard type. Three of them have been published, namely the Nippur texts HS 201 (Oelsner 2001) and Ist Ni 374 (Proust 2007: pl. 1; Friberg 2005: §4.1.10), and the Girsu text Ist L 7375 (Friberg 2007b: app. 1, fig. A1.2, and see here figure 7). Four similar texts from Umma have allegedly been found by Lafont in Istanbul (Proust 2007: 125), while the Umma tablets BM 106425 and BM 106444 (Robson 2003/2004) are of an intermediate type and share important features both with Old Babylonian tables of reciprocals and with the presumably Ur III tables of reciprocals.

Figure 7: Conformal transliteration of Ist L 7375
Remarks: the incipit has 2 igi 30; there are no entries for 1/2 and 2/3, but entries for non-regular sexagesimal numbers; variant number signs for 4, 7, 8, 40, 50; subtractive number notations for 9 and for all tens followed by 7, 8, 9; the final entry has 1 igi 1.
§4.2.2. Another table of reciprocals of roughly the same intermediate type as Robson’s BM 106444 and BM 106425a is Erm 14645 (Koslova nd: 470; photo available at CDLI under the number P211991, and see here figure 8). Figure 9 contains a comparison of characteristic features of the standard OB table of reciprocals with corresponding features of the early tables of reciprocals mentioned above.
§4.2.3. This comparison shows that only the three tables of reciprocals supposed to be from the Ur III period are written on two-column tablets and include entries for non-regular sexagesimal numbers, that is, numbers without reciprocals (expressed as n igi nu or igi n nu). Standard tables of reciprocals from the OB period include entries for two-thirds (of 60) and for half (of 60). Tables of reciprocals of the intermediate type have no entry for two-thirds (of 60) and no entries for irregular sexagesimal numbers.
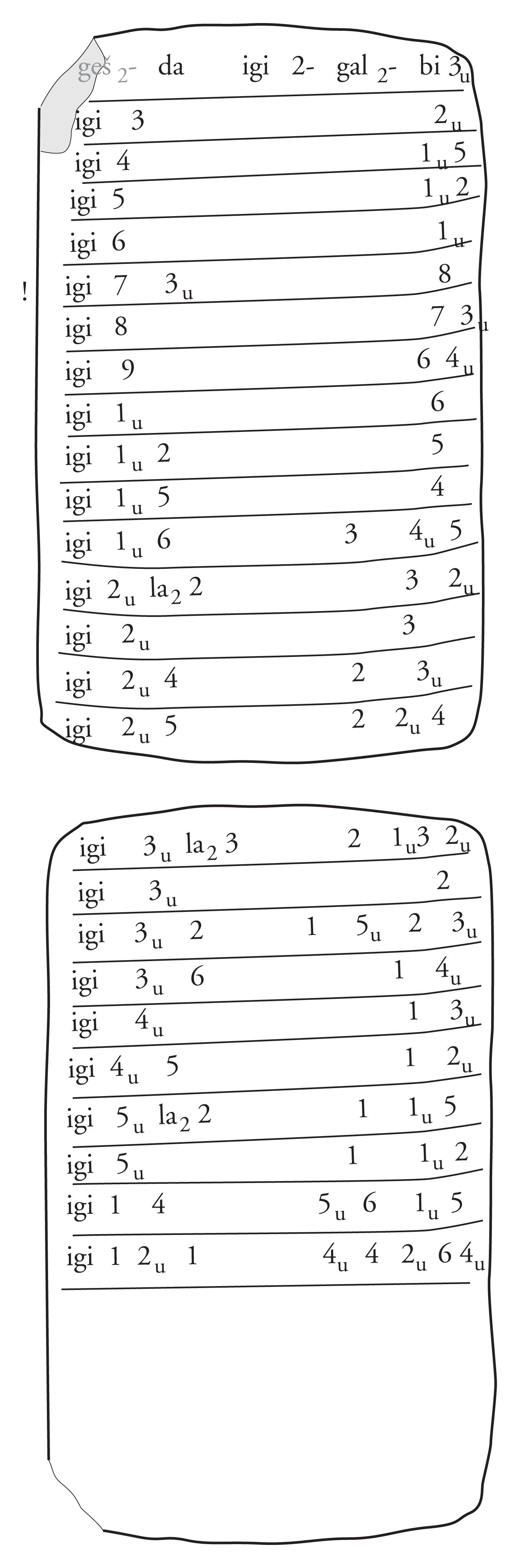
Figure 8: Conformal transliteration of Erm 14645
Remarks: the incipit has geš2-da igi 2-gal2-bi 30; there are no entries for 1/2 and 2/3, but an entry igi 7 30 = 8; final entries: igi 1 04 = 56 15, igi 1 21 = 44 26 40; missing entries: igi 54 = 1 06 40 and igi 1 = 1; no entries for non-regular sexagesimal numbers; variant number signs for 7, 8, 9, 40, 50; subtractive number notations for 9 and for all tens followed by 7, 8, and 9.
§4.2.4. There are also other interesting features of the tables of reciprocals mentioned above. In Ist L 7375, for instance, the numbers n = [7 -] 9, [17 - 19], [27 -] 29, 37 - 39, 47 - 49, and 57 - 59 are written subtractively, as 10 - 1, 30 - 1, 40 - 3, 40 - 2, 40 - 1, etc. The table ends with the entry 1 igi 1, that is with an entry for n = 1 (= 60). In the case of Ist Ni 374, no numbers are written subtractively. At the end of the table of reciprocals, after the entry [igi 1 1] for n = 1 = 60, there are no entries with irregular sexagesimal numbers, and (apparently) the table ends with an entry for n = 1 40 (= 100). In HS 201, again, the numbers n = [7 -] 9, 17 - 19, and 27 - 29 are written subtractively. The table ends, prematurely, with an entry for n = 32. In Erm 14645, with entries only for n regular, the numbers n = 18 and 48, but not 9, are written subtractively. There is one case of a non-integer n, namely n = 7 30. The table ends with entries for n = 1 04 and 1 21. The entries for n = 54 and 1 are missing, as are any entries for n regular between 1 04 and 1 21.
§4.2.5. In BM 106444, only the number n = 9 is written subtractively. There is one case of a non-integer n, namely n = 7 1/2. The entry for n = 1 (60) is written in the full form geš2-da igi 1-gal2-bi 1-am3, and the only entries after n = 1 are n = 1 04 (the 6th power of 2), 1 21 (the 4th power of 3), and 2 05 (the 3rd power of 5)! In BM 106425, no number is written subtractively. There are two non-integer entries, for n = 7 12 and 7 30, and one missing entry, for n = 48. The only entries after igi 1-bi 1 (for n = 1 = 60) are for n = 1 04 and 1 21.
§4.2.6. In the standard OB tables of reciprocals, finally, no numbers are written subtractively (not even n = 19, which in many OB multiplication tables is written as 20-1). The table ends with n = 1, 1 04, and 1 21, occasionally with inclusion also of the regular numbers between 1 04 and 1 21. The careful survey above seems to indicate that there was a lot of experimenting with different formats for the Ur III tables of reciprocals and for the tables of intermediate type, until at some time in the OB period the standard form of the OB table of reciprocals was agreed upon.

Figure 9: Comparison of the Ur III, “intermediate,” and standard OB tables of reciprocals
§5. A geometric solution model for the quadratic equation in figure 6
§5.1.1. It is known (see Høyrup 2002) that Old Babylonian mathematicians understood second degree equations as problems for the sides and areas of rectangles and squares, and that, consequently, their methods for the solution of quadratic equations were based on manipulations with rectangles and squares in terms of their sides and areas.
§5.1.2. On the other hand, it is also known that manipulations with rectangles and squares or more general quadrilaterals, occur quite frequently in the relatively small number of known “metro-mathematical” texts from Mesopotamia that can be dated to various parts of the millennium preceding the Ur III period. Notable examples of such “metric algebra” are applications of the “proto-literate field-expansion procedure” in some proto- literate field-sides and field-area texts from around 3200 BC (Friberg 2007b: §8.1 c), computations of the area of a very large square and computations of the areas of several series of squares or rectangles in texts from the Early Dynastic III period, around 2600–2500 BC (Friberg 2007b: ch. 6 and app. 7), as well as applications of the field expansion procedure, complicated computations of areas of squares, and solutions to square-side and -area exercises in Old Akkadian texts from around 2340-2200 BC (Friberg 2007b: app. 6).
§5.1.3. Therefore, if it is correct, as suggested by the evidence of the juridical document YBC 3879, that it was known already in the neo-Sumerian period how to set up and solve quadratic equations, then there is every reason to believe that solutions to such equations were obtained in the Ur III period through manipulations with squares and rectangles, in precisely the same way as in the Old Babylonian period two or three centuries later.
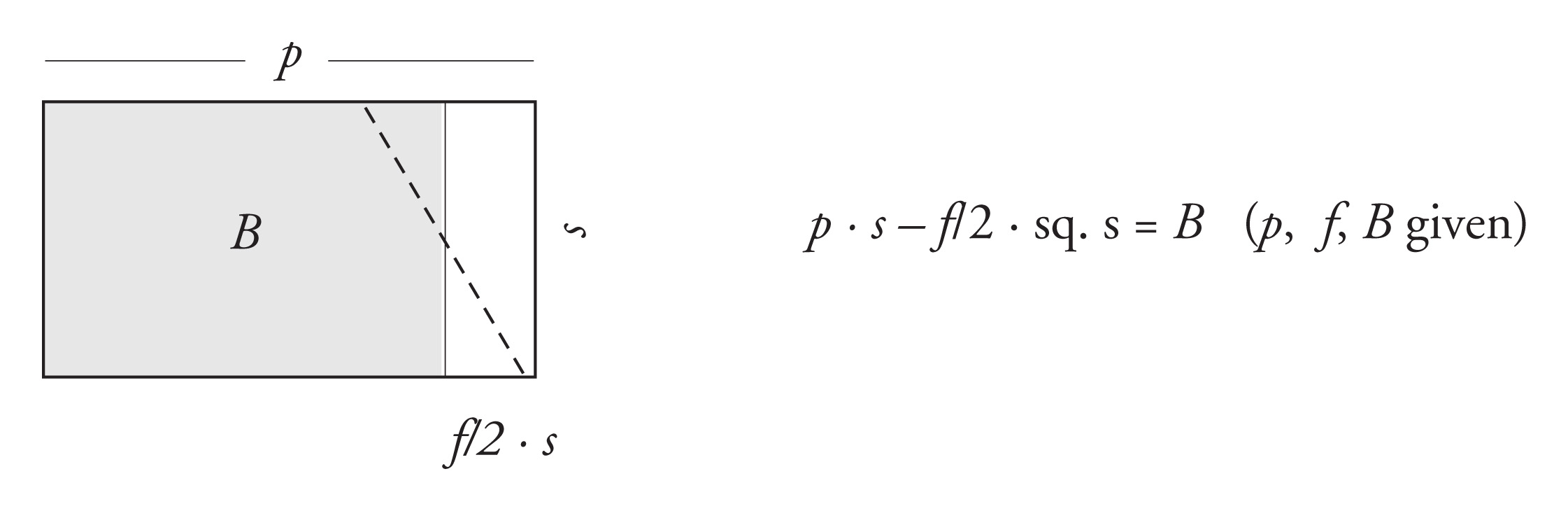
Figure 10: The general form of a quadratic equation like the one in figure 6 above.
§5.2.1. Take, specifically, quadratic equations of the type apparently used repeatedly for the solution of the field division problem in YBC 3879 (see the example in figure 6 above). In quasi-modern notations, equations of this type can be written in the form
p · s - f/2 · sq. s = B,
where s is an unknown length number, p a given length number, f a given numerical constant (the “feed” of a certain trapezoid), and B a given area. However, in geometric terms, the equation can be interpreted as saying that if a rectangle with sides of the lengths s and f/2 · s is removed from a rectangle with the sides p and s, then what remains is a rectangle of given area B. The situation is illustrated by the diagram in figure 10.
§5.2.2. The first step in the geometric solution procedure will then be to transform the given problem to a geometrically expressed quadratic equation of one of several possible standard types. See the list of Old Babylonian “basic metric algebra problems” in Friberg 2007a: 6. The appropriate basic metric algebra problem in the case considered here is a “quadratic equation of type B4c,” which, in quasi-modern notations, is of the form
2 p · b - sq. b = F, where b = f · s and F = f · 2 B.
§5.2.3. Geometrically, a quadratic equation of type B4c corresponds to the situation when a square with a side of unknown length, call it b, is removed from a rectangle with a given side of length 2 p and the other side of length b, and what remains is a rectangle of given area F. The situation is illustrated by the diagram in figure 11.
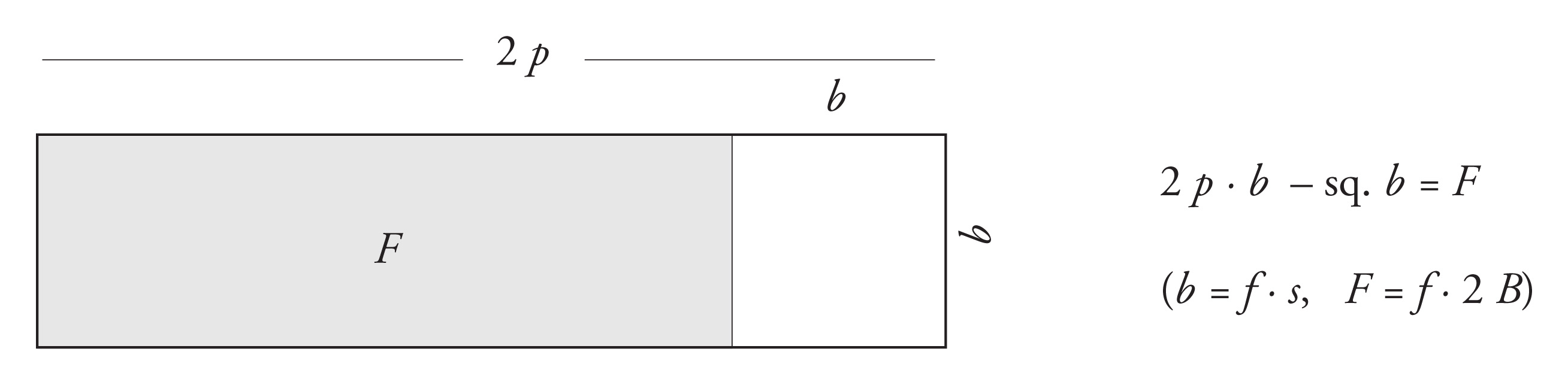
Figure 11: Transformation of the equation in figure 10 into a quadratic equation of type B4c.
§5.2.4. In geometric terms, the transformation of the problem in figure 10 into a quadratic equation of type B4c (figure 11) can be performed as follows: The length of the diagram in figure 10 is scaled up by the factor 2, at the same time as the front (= width) of the diagram is scaled down by the factor f. In this way, the removed rectangle with the sides f/2 · s and s is transformed into a square with the new unknown side b = f · s, at the same time as the remaining rectangle is transformed into a rectangle with the new known area F = f · 2 B. (Alternatively, and perhaps more in line with known examples from Old Babylonian mathematical problem texts, the length remains unchanged, while the front is scaled down by the factor f/2.)
§5.2.5. The next step in the geometric solution procedure is to transform the diagram in figure 11 into a “square difference” or “square corner” (Greek: gnomon), that is, into the case when a square located in a corner of a bigger square has been removed from that square. One way in which this can be done is shown in figure 12 below. Consider a “ring of four rectangles” with the side 2 p and the width b as in figure 12, left. Then each one of the four rectangles has the known area F. Consequently, F is one quarter of the area of the whole ring of rectangles. Another way of dividing the ring of rectangles into four pieces of area F is shown in figure 12, right, where the ring of rectangles is divided into four square corners of area F. The construction shows that if a square with the side p - b is removed from a square with the side p, what remains is a square corner with the area F. In other words,
sq. p - sq. (p - b) = F
so that
sq. (p - b) = sq. p - F.
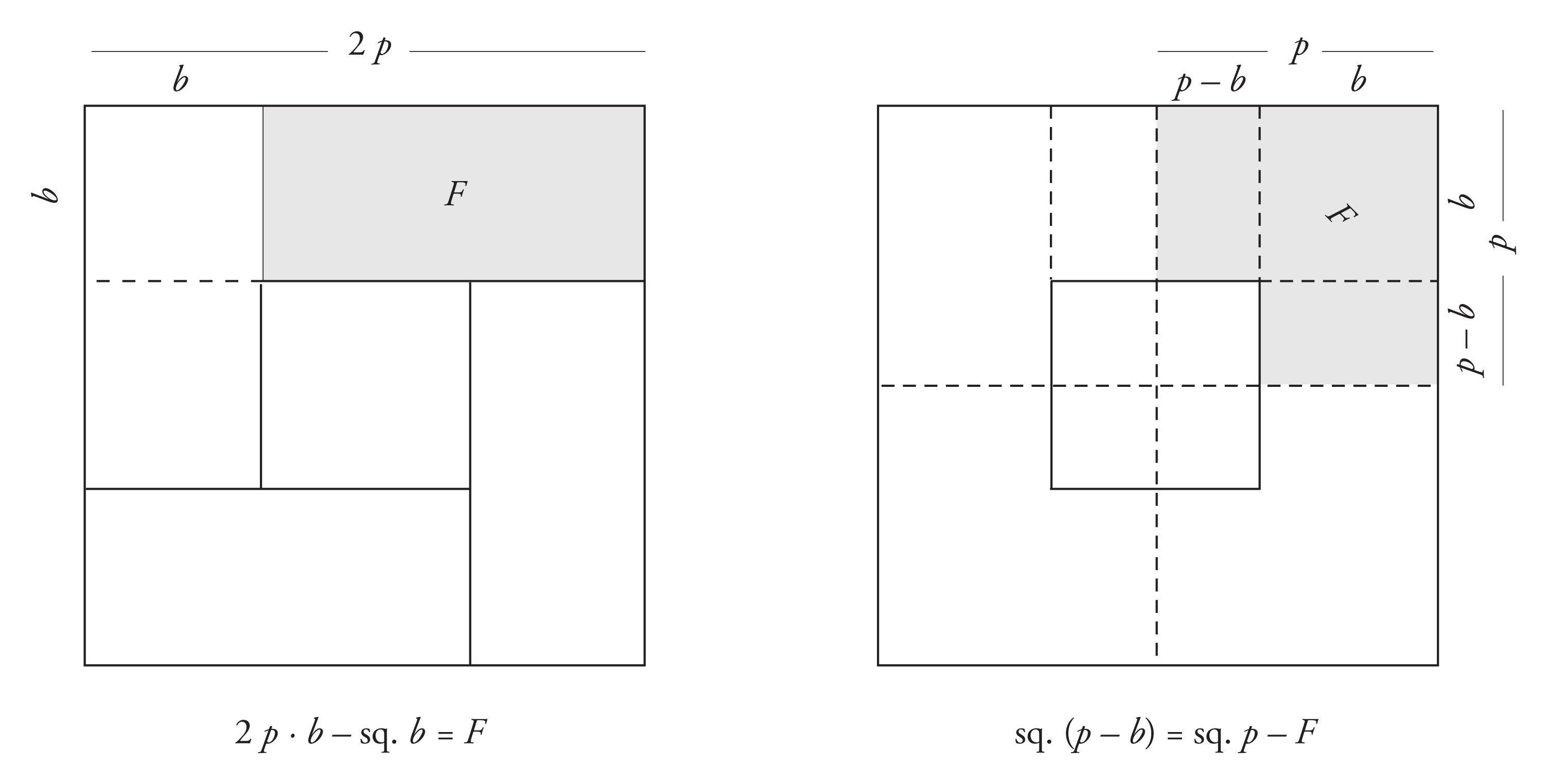
Figure 12: Solving a quadratic equation of type B4c through “completion of the square”.
Remarks: There is only circumstantial evidence that Old Babylonian mathematicians used rings of rectangles in this way to solve quadratic equations. What is known, however, is that they worked with rings of three trapezoids and with rings of four right triangles. See the discussion in Friberg 2007b: §§2.4.
§5.2.6. Since both p and F are assumed to be known, it follows that also the area of the square with the side p - b is known. Therefore, the length of p - b can be computed as the corresponding square side. Since p is known, b can then be computed, and the problem is solved. The method described above is, of course, the method of “completion of the square,” manifestly here in its true, geometric sense.
§6. An alternative solution method for the problem in figure 6
§6.1. In the argumentation for the surmised Babylonian origin of certain geometric constructions in Book II of Euclid’s Elements (Friberg 2007a: §§1.2-1.3) it is shown how quadratic equations of various forms can be replaced by equivalent “rectangular-linear systems of equations”. In the same place are discussed examples of rectangular-linear systems of equations appearing in both Old and Late Babylonian problem texts.
§6.1.1. In agreement with the mentioned possibility to replace a given quadratic equation by a mathematically equivalent rectangular-linear system of equations, it will now be shown how the author of YBC 3879 conceivably may have solved his field division problem by use of rectangular-linear systems of equations, rather than by use of quadratic equations as suggested in the preceding sections of this paper.

Figure 13: A diagram expressing either a quadratic equation or a rectangular-linear system.
§6.1.2. Thus, consider again the geometrically expressed equation for the second partial front s2 as in figure 13. The “metric algebra diagram” in figure 13 can be interpreted in two mathematically equivalent ways. Firstly, it can be interpreted as follows (cf. figure 6 above) as a quadratic equation for the front s2 plus a linear equation for the length u3':
u2' · s2 - f/2 · sq. s2 = A/5, u3' = u2' - f · s2, with u2', f, and A/5 given.
As shown above, these equations can be rewritten in the following simplified form:
2 u2' · b2 - sq. b2 = f · 2 A/5, u3' = u2' - b2, where b2 = f · s2.
Through completion of the square, etc., the solution is then obtained in the form
sq. u3' = sq. u2' - f · 2 A/5, b2 = u2' - u3', s2 = 1/f · b2 (*)
§6.1.3. Alternatively, the diagram in figure 13 can be interpreted in the following way as a rectangular-linear system of equations for the two unknowns s2 and u3':
(u2' + u3')/2 · s2 = A/5, u2' - u3' = f · s2, with u2', f, and A/5 given (**)
Here, too, the equations can be rewritten in a simplified form, namely as
(u2' + u3')/2 · b2/2 = f/2 · A/5, (u2' + u3')/2 + b2/2 = u2', where b2 = f · s2.
This is (see Friberg 2007a: 6) a rectangular-linear system of type B1a for the two unknowns (u2' + u3')/2 and b2/2. As such, the system of equations can be solved by use of a “completion of the square” similar to the one in figure 12.

Figure 14: A geometric proof of the conjugate rule (p + q) · (p - q) = sq. p - sq. q.
§6.1.4. Interestingly, there is another, and apparently simpler way of solving the system of equations (**) above in this particular case. Indeed, if the first equation is multiplied by 2 f, and if then the product f · s2 is replaced by u2' - u3', the result is the following quadratic equation for a single unknown u3':
(u2' + u3') · (u2' - u3') = f · 2 A/5,
with u2', f, and A/5 given. Through an application of the “conjugate rule” this equation for u3' can be simplified to
sq. u2' - sq. u3' = f · 2 A/5.
In this way, the use of a “completion of the square” can be entirely avoided, yet the end result is the same as before! (Cf. the solution in the form (*) above.)
§6.1.5. However, the apparent simplicity of a solution of (**) by way of the conjugate rule, as contrasted with a solution by way of a completion of the square, is deceptive. Indeed, a simple metric algebra proof of the conjugate rule (displayed in figure 14) makes use of a ring of rectangles just as the proof by completion of the square in figure 12. This means, somewhat unexpectedly, that there exists a close connection between the geometric form of the proof of the conjugate rule and the geometric form of a proof by completion of the square!

Figure 15: YOS 1, 23 = YBC 3901. A field plan text from Umma. Hand copy: A. T. Clay.
§6.2.1. Now, consider again the situation in figure 13, where the known quantities are the length u2', the area A/5, and the “feed” f, while the unknown quantities are the lengths u3', s2, and b2 = f · s2. As was shown above, all that is needed in order to find the values of those unknowns are simple applications of the area rule for a trapezoid, of the concept of the “feed” of a trapezoid with a sloping side, and of the conjugate rule, plus, of course, some quite laborious numerical calculations.

Figure 16: YBC 3901, obv., drawn to scale.
§6.2.2. In this connection, it may be appropriate to point out that geometric versions of the following two forms of the “binomial rule”
sq. (p + q) = sq. p + 2 p · q + sq. q and
sq. (p - q) = sq. p - 2 p · q + sq. q,
seem to have been well known in Mesopotamia already in the Old Akkadian period, that is well before the Ur III period (cf. Friberg 2005, figures 10 and 12). Therefore, it is reasonable to assume that also the conjugate rule was known in Mesopotamia in, or even before, the Ur III period.
§7. YOS 1, 23 = YBC 3901, another field plan text from Ur III Umma
§7.1. Together with the important juridical document / field plan text YBC 3879, Clay published several other field plan texts, less complicated than YBC 3879. One of them, YOS 1, 23 = YBC 3901, is historically important in its own way, as will be shown below.
§7.2. YBC 3901 is inscribed on the obverse with the plan of a field. On the reverse, there is another, quite simple, field plan, and a record of the total areas of the fields depicted in the two field plans. The field shown on the obverse is divided into five sub-fields. See the hand copy in figure 15. The four lower sub-fields are all trapezoidal, and they fit roughly together to form a larger trapezoid. The uppermost sub-field is a small triangle. The sides of the sub-fields are recorded in the field plan, as multiples of the main length unit ninda “pole?” and the fractional unit kuš3 “cubit” (= 1/12 ninda). The areas of the five sub-fields, correctly computed as (non-positional!) sexagesimal multiples of the area unit sar (= 1 square ninda), are recorded immediately to the right of the field plan.
§7.3. The copy of the field plan in figure 16 with transliterations of the cuneiform length and area numbers is drawn to scale. As shown in figure 16, right, the sum of the area numbers for the five sub-fields, counted from the bottom up, is
46(60) 46 2/3 sar = 1(bur3) 1(eše3) 4(iku) 6 2/3 sar.
In the cuneiform script, the area units figuring here, namely the iku (= 100 sar), the eše3 (= 6 iku), and the bur3 (= 3 eše3), are written each with its own kind of number signs (see the factor diagram for system A(Ur III) in §2 above). The sum is recorded in the summary on the reverse of YBC 3879, as
1(bur3) 1(eše3) 4 1/2 1/4 (iku), where 1/2 1/4(iku) = 75 sar.
§7.4. The mistake can, possibly, be explained as follows: On the obverse, the area of the uppermost trapezoidal sub-field is written as 3(60) 47 X sar, where X, which should be the usual cuneiform sign for 2/3, looks more like the combined sign for 1/2 1/4(iku) (see again the factor diagram for system A(Ur III) in §2 above). Therefore, when the author of the text computed the sum of the areas of the sub-fields, he seems to erroneously have read X as 1/2 1/4(iku) and then rounded off the result by not recording the final 6 sar.
§8. The importance of YOS 1, 23-24, for the history of mathematics
§8.1.1. By some quirk of fate, there are almost no known mathematical cuneiform texts from the Sumerian Ur III period, although the number of known nonmathematical cuneiform texts from the Ur III period is enormous, and although there are several known mathematical cuneiform texts from the Old Akkadian and Early Dynastic periods which preceded the Ur III period. An important exception, so far, has been several tables of reciprocals (see §4 above) which are so unlike the standard type of Old Babylonian tables of reciprocals that it seems to be justified to assume that they are from the Ur III period.
§8.1.2. Another exception is AO 5499, a well preserved text from the city Drehem, dated to the 48th regnal year of the king Šulgi, which contains a painstakingly detailed arithmetical algorithm accounting for the theoretical growth over a period of ten years of a cattle herd consisting, at the outset, of four milk cows, with an account of also the resulting output of dairy fat and “cheese” and the corresponding value in silver (see Nissen, Damerow, and Englund 1990: 97-102, in particular the schematic diagram in their figure 78). AO 5499 pretends to be a normal bookkeeping document. Thus, the result of each step of the computational algorithm is presented as an account for a certain year, mentioning the year formula for that year, and in a subscript the whole text is said to be an “account of Idūa, son of Issu-arik, the manager of the temple of the deity Ištaran”. Moreover, standard Ur III capacity and weight numbers are used for the recorded amounts of dairy fat and “cheese” and for the corresponding amounts of silver. On the other hand, typically for a mathematical exercise, the calculations in the document are based on a number of simplifying but unrealistic assumptions, in particular a mortality rate of zero among the cattle.
§8.1.3. Another example of what may be a neo-Sumerian mathematical text in disguise is YBC 9819 (Robson 1999 68; Friberg 2001: 134) which Robson 1999: 68 calls “an Ur III school text in the form of a model document (which) purports to be about bricks for the walls of the temples of Šara and Ninurra in Umma”. This text is a rather detailed account of bricks needed to build a number of walls, some made of square 1/3-cubit-bricks, in the text called ukurrum (elsewhere agurrum) bricks, and others made of square 2/3-cubit bricks, in the text called zarin bricks. In both cases, an extra fifth is added to the thickness of normal bricks (5 fingers), which presumably is what is indicated by the obscure phrase igi 5-gal2 ugu2 ba-an-ni-ib2-gal2 “there is an ugu of 1/5.” The corresponding “molding numbers” for the two numbers of bricks should be 10 48 · 5/6 and 2 42 · 5/6 (brick-sar per volume sar), respectively, but both molding numbers are incorrectly calculated by the author of the text (Robson 1999). The structure of the text is complicated. First the total amounts of ukurrum bricks and zarin bricks for the walls of the two temples are listed separately, then the grand totals of the two kinds of bricks for the walls of both temples together. The school text character of the account is suggested, among other things, by the fact that the sum of the two grand totals
19 bur3 2 eše3 4 1/2 iku 3 1/2 sar = (appr.) 20 bur3 - 1/2 iku
is very close to the round number
20 brick-bur3 = 10 šar2 brick-sar
= 10 · (60 · 60) · (12 · 60) bricks
= 2 · 60 · 60 · 60 · 60 bricks.
§8.1.4. Thus, the reason for the nearly total absence of known mathematical cuneiform texts from the Ur III period in Mesopotamia may be that mathematical texts from that period often, just like AO 5499 and YBC 9819, are cleverly disguised as administrative accounts of one type or another. In particular, most mathematical cuneiform texts from the Ur III period can be expected to be “metro-mathematical” like all other known mathematical cuneiform texts from the third millennium BC. The term means that all such texts are combinations of mathematical and metrological exercises, unlike Old Babylonian mathematical texts which are often purely mathematical, counting with abstract sexagesimal numbers in place value notation.
§8.2.1. The juridical document YOS 1, 24 = YBC 3879 discussed in §1 above seems to confirm this conjectural characterization of mathematical texts from the Ur III period. It is certainly metro-mathematical, expressing all lengths and areas in terms of standard units for length and area measure, but at the same time making use of relatively complicated mathematical techniques. As remarked in the introductory §1.1, it contains the first documented appearance of solutions to metric algebra problems of the second degree in a pre-Babylonian text, and also the first documented appearance of a geometric algorithm in a pre-Babylonian text. (An “algorithm” is a solution procedure consisting of a series of consecutive steps, each step similar to the one before it and making use of the result of the computations in the preceding step.) YBC 3879 is also the earliest known cuneiform text making use of the concept “feed” (related to the modern concept “inclination”), although only implicitly. Note, by the way, that in YBC 3879 the “feed” is of the very simple form 1/5 1/3 · 1/5 (in sexagesimal place value notation = ;16), a circumstance which may be an indication that YBC 3879 is a school text with fabricated data. It is also interesting to note that the recorded results of the calculations in the text are unrealistically detailed, as is often the case in mathematical cuneiform texts. Indeed, what is the sense of expressing the sides of the five parallel stripes into which the orchard is divided in so and so many ninda, cubits, and fingers?

Figure 17: AO 6060. A field plan from Umma, and the same field plan drawn to scale.
§8.2.2. It is, of course, equally likely that YBC 3879 from the beginning was what it appears to be, namely a juridical document, recording the outcome of a legal process about how to divide an existing date-grove between five named persons into five stripes of equal area. Ultimately, on the other hand, copies of that original juridical document may have been used for school purposes as a “model text” for mathematical problems of the type “division of inheritance between 5 sons”. Whatever the case may be, the original author of the text must have had some training in school in how find the solutions to certain metric algebra problems of the second degree.
§8.2.3. A potentially important observation is that the division problem on YBC 3879 may pro vide a long missing answer to the question how metric algebra problems of the second degree became part of the Old Babylonian mathematical tradition. As was shown above, any division of property question in which a trapezoidal field is to be divided into parallel stripes in certain proportions will automatically lead to one or several problems of the second degree. Such situations cannot have been particularly uncommon.
§8.3.1. YOS 1, 23 = YBC 3901 (figure 16) appears to be a bona fide field plan text, concerned with a considerably less sophisticated division of a field into five subfields. Note that the lengths of the five transversals, 12 n. 2 c., 16 n. 3 c., 24 n. 3 c., 32 1/2 n. 2 c., and 41 n., do not form a geometric progression with a constant increase in length from one transversal to the next. That means that the lengths may have been measured, rather than calculated.
§8.3.2.1. Another field plan text of a similar type is AO 6060 (Nissen, Damerow, and Englund 1990: 68 and figure 57; figure 17 here), where a field is divided into six sub-fields of various areas. Note that, just like the field plan on YBC 3879, rev., the field plan on AO 6060, obv., seems to be an incorrect copy of a more accurately drawn field plan on another clay tablet, since the triangular sub-field at the top of the field plan is not correctly drawn.

Figure 18: MS 1938/2. A presumably neo-Sumerian mathematical hand tablet.
§8.3.2.2. One notable difference between YBC 3901 and AO 6060 is that in the field plan on AO 6060, obv., the sub-areas are expressed in standard area number notations, as multiples of the iku, eše3, and bur3, while in the field plan on YBC 3901, obv. the sub-areas are expressed as multiples of the sar = square ninda, with 18(60) 25 sar instead of 1(eše3) 5(iku) 5 sar, 14(60) 14 sar instead of 1(eše3) 2 1/2(iku) 4 sar, etc. In this respect, YBC 3901 is closer to the style of Old Babylonian mathematical cuneiform texts, where standard area number notations are used only in the answer, if at all, while sexagesimal multiples of the square ninda (never explicitly mentioned) are used in all the preceding computations.
§8.4.1. A third field plan of a similar kind is MS 1938/2, obv. (Friberg 2007b: figure 8.1.12; here figure 18). Friberg remarked about this text (2007b: 201) that
Although MS 1938/2, obv. with its drawing of a striped trapezoid and its series of area numbers looks like a field plan, it is more likely that the text is the answer to an assignment, possibly an inheritance problem for “six brothers.” Normally, trapezoids in drawings on Old Babylonian clay tablets are positioned with the long sides (the “lengths”) extending from left to right, and with the “upper front” to the left and the “lower front” to the right. However, judging from the way in which most of the numbers are written, the trapezoid on the obverse of MS 1938/2 may very well have been oriented in an unusual way, with what is normally the (longer) upper front facing downwards. MS 1938/2 is also unlike normal Old Babylonian hand tablets with geometric exercises in that the computed areas are expressed in terms of area numbers rather than sexagesimal numbers in relative place value notation. A possible explanation is that MS 1938/2 is a Sumerian rather than Old Babylonian geometric exercise!
This statement appears confirmed by the fact that the field plan on MS 1938/2 (of unknown provenience) closely resembles the field plans on YBC 3901 and AO 6060, both Sumerian Ur III texts from Umma.
§8.4.2. The reason for assuming that MS 1938/2, obv. is the answer to a mathematical assignment, rather than a bona fide field plan, is the observation that in this text all the six sub- fields of the divided field have the same partial length, 1(60), with the result that their widths (counted from the base) form a descending arithmetic progression, 1(60) 10, 1(60), 50, 40, 30, 20, 10. This kind of conspicuously nice data is typical for mathematical texts.
§8.4.3. Independently, the assumption that MS 1938/2 is a mathematical text is confirmed by the circumstance that undoubtedly the diagram on the reverse of MS 1938/2 is mathematical. The (reconstructed) diagram shows a circle inscribed in the middle of a “6-front” (regular hexagon), some distance away from that figure. See the discussion of MS 1938/2, rev. in Friberg 2007b: §8.2
e-f, together with a discussion of three Old Babylonian mathematical texts with a square in the middle of a square, a circle in the middle of a square, and a “concave square” in the middle of a square or in the middle of a rectangle.
§8.5.1. Conclusion: The previously so embarrassing apparent absence of mathematical cuneiform texts from the Sumerian Ur III period is no longer quite as absolute as before. In addition to three presumably Ur III tables of reciprocals HS 201, Ist Ni 374, and Ist L 7375 (plus, perhaps, the four tables of reciprocals allegedly found by Lafont), and the algorithm text for a herd of cattle AO 5499, there are also the juridical document / field plan text YBC 3879, the field plan plus a circle-in-a-6-front text MS 1938/2, and possibly the two field plan texts YBC 3901 and AO 6060.
§8.5.2. The Umma tablets BM 106444 and BM 106425 published by Robson 2003/2004, as well as the previously unpublished tablet Erm 14645 (§4.2.2 above), strangely display some features typical for Old Babylonian tables of reciprocals and other features typical for Ur III tables of reciprocals, which probably means that they represent some kind of “missing link” between the two types of cuneiform tables of reciprocals.
§8.5.3. Three additional mathematical texts presumably from the Ur III period are mentioned in the recently published work Proust 2007. Two such texts are the combined multiplication table Ist Ni 5173 and the single multiplication table Ist Ni 2208, both from Nippur, both making use of archaic forms of some number signs, and both apparently produced by accomplished scribes rather than by school boys (Proust 2007: 134). Another text with pronounced archaic features is the small tablet AOT 304 (Proust 2007: 212) with a problem for a pile of bricks on the obverse, and with sexagesimal numbers in place value notation on the reverse. It was claimed to be from Ur III already by Thureau-Dangin 1903. An interesting analysis of this text was made by Robson 1999: 66.
§8.5.4. As some of these examples show, there are reasons to believe that additional Neo-Sumerian mathematical cuneiform texts may have been published already but are hiding behind incorrect classifications as administrative Ur III documents, or as Old Babylonian mathematical texts. Note also, in this connection, that the famous Old Babylonian table text Plimpton 322 with its systematically arranged set of data for a certain kind of quadratic equations (Friberg 2007b: app. 8) was originally classified as a “commercial account” (Neugebauer and Sachs 1945: 39), and that the Old Akkadian mathematical problem text CMAA 16-C0005 with its “metric division exercise” ( Friberg 2005: §2.1) was originally sold at an online auction as an Old Babylonian (sic!) “shoemaker’s account.”
§9. The earliest known example of a quadratic problem in a cuneiform text
§9.1. In a brief account of “the discovery of Babylonian ‘algebra’” in the introduction to his book LWS (2002, p. 1, fn. 2), J. Høyrup writes that
... By the end of the 1920s it was thus accepted that Babylonian mathematics could be spoken of on an equal footing with Egyptian mathematics ... . Nonetheless it came as an immense surprise in the late 1920s when Babylonian solutions of second-degree equations were discovered at Neugebauer’s seminar in Göttingen. Until then, systematic treatment of second-degree algebra was believed either to begin with the Indian mathematicians and then to have been borrowed by the Arabs; with Diophantos; or, in geometric disguise, with Euclid (Elements II) and Appolonios.
Indeed, in 1985, Høyrup was told in a private conversation with Kurt Vogel, one of the pioneers of the study of Babylonian mathematics, about the “immense amazement with which the discovery was received.” The first publications relating to the discovery appeared in the first volume of Neugebauer’s series Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik (1929), where Neugebauer and Schuster wrote about solutions to quadratic equations in Old Babylonian and Seleucid mathematical cuneiform texts, respectively.
§9.2. It is ironical that the juridical document YBC 3879 with its solutions to a series of quadratic problems was published by Clay in 1915, more than a decade before the mentioned surprising discovery of solutions to quadratic equations in Babylonian mathematical texts. Yet the unexpected conclusion drawn in the present paper, based on a detailed and pains taking study of YBC 3879, that quadratic equations could be set up and solved (in one way or another) already in the Sumerian Ur III period, may still not be the end of the story. Actually, it is in no way unlikely that the study of quadratic equations (or of mathematically equivalent rectangular-linear systems of equations) was part of the education in mathematics in the Old Akkadian period, maybe even before that, in the Early Dynastic period.
§9.3. Although this hypothesis is still very bold and tentative at the present stage of our knowledge about mathematics in Mesopotamia in the 3rd millennium BC, it is supported by, among other things, the following observation:
§9.3.1. IM 58045 (Friberg 2007a: §11.3a; here figure 19) is a round mathematical hand tablet securely dated to the Old Akkadian period (five hundred years before the Old Babylonian period), since it was found in the ruins of a collapsed house together with explicitly dated administrative documents. The diagram on the obverse of IM 58045 shows a trapezoid divided into two parallel stripes by a transversal parallel to the fronts of the trapezoid. The two fronts are given as 3 reeds - [1 cubit] and 1 reed 1 cubit, respectively. Since 1 reed = 6 cu bits, this means that the fronts are 17 and 7 cubits. The length (or height) of the trapezoid is given as 2 reeds = 12 cubits (= 1 ninda). Consequently, the area of the whole trapezoid is
A = 12 cubits · (17 cubits + 7 cubits)/2 = sq. (12 cubits) = 1 sq. ninda = 1 sar.

Figure 19: IM 58045. An Old Akkadian hand tablet showing a bisected trapezoid.
§9.3.2. This nice choice of data, and the diminutive size of the field (only 1/100 iku), show that IM 58045 is a mathematical text, rather than an ordinary field plan text. Moreover, geometric diagrams of this type are well known from Old Babylonian mathematical texts (for a detailed documentation, see Friberg 2007a: §11.3b-f), where they describe situations when a trapezoid is bisected by a transversal parallel to the fronts into two parallel stripes of equal area, and where the position and the length of the transversal are asked for. In the standard example of a “trapezoid bisection problem” of this kind, the lengths of the two fronts are proportional to the pair 17, 7, just as in the case of IM 58045.
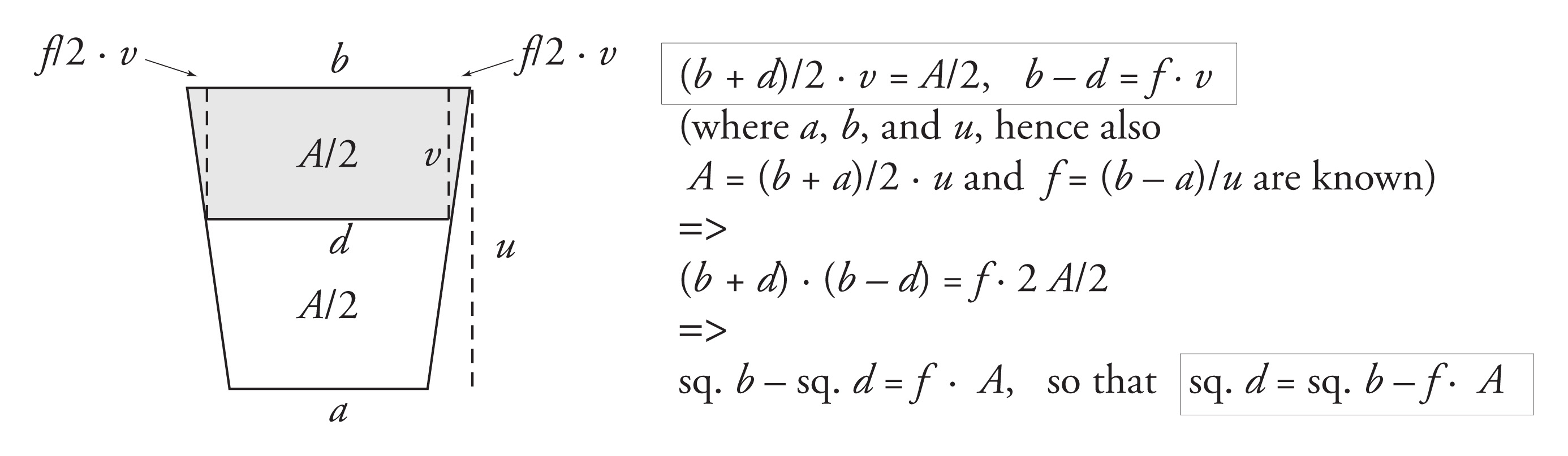
Figure 20: A solution to the trapezoid bisection problem by use of metric algebra.
§9.4. It is likely that the diagram on IM 58045 was an assignment, in the sense that a school boy took the hand tablet with the diagram with him home from school one day and was expected to return to school the next day, handing in to the teacher the solution to the trapezoid bisection problem with the data recorded on the hand tablet.
§9.5. Now, observe that the Old Akkadian trapezoid bisection problem with the data recorded on IM 58045 is closely related to the neo-Sumerian field division problem solved on the obverse of YBC 3879. Indeed, consider generally, as in figure 20, a trapezoid with the two given fronts b and a and the given length (or height) u.
§9.6. By use of the alternative solution method discussed in §6 above, the length d of the traversal dividing the trapezoid in two parts of equal area can be computed as follows: Let A be the area of the trapezoid, and let f be its “feed.” Then
(b + d)/2 · v = A/2 and b - d = f · v, where v is the partial length (or height).
Consequently,
(b + d) · (b - d) = f · A
so that, in view of the conjugate rule, d can be computed as the solution to the equation
sq. b - sq. d = f · A.

Figure 21: MS 3052 no. 1: A wall where material from the top has been used to make the wall longer.
§9.7. In a precisely parallel way, it can be shown that sq. d - sq. a = (d + a) · (d - a) = f · A. An important consequence of this pair of similar equations is that
sq. b - sq. d = sq. d - sq. a.
Consequently, d can also be computed as the solution to the following equation
sq. d = (sq. b + sq. a)/2, “the trapezoid bisection rule”.
With the data given in the Old Akkadian text,
b = 17 c., a = 7 c., u = 12 c. => f = (17 - 7) c. /12 c. = 10 · 1/12, A = sq. (12 c.). Hence, sq. d = sq. (17 c.) - 10 · 1/12 · sq. (12 c.) = (4(60) 49 - 2(60)) sq. c. = 2(60) 49 sq. c. = sq. 13 c., d = 13 c.
Alternatively,
sq. d = (sq. 17 c. + sq. 7 c.)/2 = (4(60) 49 + 49)/2 sq. c. = 2(60) 49 sq. c. = sq. 13 c., d = 13 c.
§9.8. It is, of course, not known precisely which method the Old Akkadian schoolboy was supposed to use to solve the problem set in his assignment. Note, by the way, that it is only because the values 17 c. and 7 c. for the fronts were appropriately chosen that the square side of (sq. 17 c. + sq. 7 c.)/2 turned out to be an integral multiple of 1 cubit. In other words, b, d, a = 17, 13, 7 is a solution in integers to the indeterminate quadratic equation
sq. b + sq. a = 2 sq. d.
How this remarkable property of the triple 17, 13, 7 may have been discovered by some mathematician living in Mesopotamia in the Old Akkadian period, or maybe even earlier, is described in Friberg, 2007a: §11.3 a.
§10. Old Babylonian applications of the alternative trapezoid area rule
§10.1. In §§3 and 6 above, it was explained how the author of YBC 3879 = YOS 1, 24 may have computed, for instance, the second partial front s2 of the divided orchard in the following way (with notations as in figure 13):
sq. u3' = sq. u2' - f · 2 A/5, b2 = u2' - u3', s2 = 1/f · b2 (*)
Here u2' is a given length, f a given “feed” (inclination), and A a given area. It was also explained in §§3 and 6 how the author of the text may have found the equation for the length u3' by solving either a quadratic equation or a rectangular-linear system of equations. Note, however, that it is not necessarily true that the author of the text (who may have been a surveyor, rather than a mathematician) knew how to solve such equations. All he needed to know was a rule for computing one of the parallel sides of a trapezoid when the other parallel side, the “feed” of the trapezoid, and the area of the trapezoid were known. In Friberg 2007b: 284, a rule of this kind was called the “Old Babylonian alternative trapezoid area rule”. In view of what has appeared above, a more appropriate name may be simply the “Mesopotamian alternative trapezoid area rule.”
§10.2.1. Three examples of the application of this rule in Old Babylonian mathematical cuneiform texts are known. The first example occurs in YBC 4675 (Friberg 2007a: 273), where a (quasi-) trapezoid has the given fronts sa = 17 and sk = 7, and the given lengths 5 10 and 4 50 (ninda). Asked for is the length d of a transversal parallel to the fronts which divides the trapezoid into two sub-trapezoids, both with the area A/2 = 1 bur3 (= 30 00 sar). The problem is solved through computation of first the average length,
u = (5 10 + 4 50)/2 = 5 (in relative sexagesimal numbers),
then the corresponding “feed,”
f = (17 - 7)/5 = 10/5 = 2,
and finally the square of the transversal by use of the alternative trapezoid area rule,
sq. d = sq. sa - f · 2 A/2 = sq. 17 - 2 · 2 · 30 = 4 49 - 2 = 2 49, so that d = 13.
§10.2.2. A second Old Babylonian example can be found in MS 3052, another Old Babylonian problem text from Uruk, where in problem no. 1 (Friberg 2007b: 258; here figure 21) a wall with a trapezoidal cross section has the given length u = 3 00 ninda, the given height h = 1/2 ninda (= 6 cubits), and the given widths sk = 3 cubits (= ;15 ninda) at the base and sa = 1/3 cubits (= ;01 40 ninda) at the top, respectively. (The wall is said to be ana muḫḫim suḫḫur “turned back at the top,” where, apparently, suḫḫur is the Akkadian counterpart to the Sumerian term ba-gi4!) Material is taken from the top of the wall in or der to make the wall p = 20 ninda longer. How much lower (ha) will then the wall become?

Figure 22: MS 2792 no. 2. A sloping ramp constructed by four teams of soldiers.
§10.2.3. The successive steps of the numerical solution procedure are the following:
A = (15 + 1 40)/2 · 6 = 50,
V = A · u = 50 · 3 = 2 30,
Ak = A · u / (u + p) = 2 30 / 3 20 = 45‚
f = (15 - 1 40) / 6 = 13 20 / 6 = 2 13 20,
sq. d = sq. sk - f · 2 Ak = sq. 15 - 2 13 20 · 2 · 45 = 3 45 - 3 20 = 25,
d = 5 (1 cubit)‚
ha = (d - sa) / f = (5 - 1 40) / 2 13 20 = 3 20 · 27 = 1 30 (1 1/2 cubits).
§10.2.4. A third Old Babylonian example can be found in MS 2792, a problem text from Uruk, where in problem no. 2 (Friberg 2007b: 288; here figure 22) four sections of a sloping ramp have been constructed by four teams of “soldiers.” The work with the construction of the four sections has required 4 30, 8 00, 6 40, and 7 30 “man-days,” respectively. The given length of the ramp is 13;20 (ninda), the given heights of the ramps at the two ends are ha = 23;20 and hk = 10 (cubits). Asked for are the lengths of the four sections.
§10.2.5. The lengths of the four sections are computed in four steps by means of a geometric algorithm which begins with the computation of the length of the first section. In this first step of the algorithm are computed in the following way the area A of the vertical side face of the whole ramp, the total number E of “man-days,” the area A1 of the vertical side face of the first section, the “feed” f of the trapezoidal side face, the length d1 of the first transversal, and finally the length u1 of the first section:
A = 13 20 · (23 20 + 10)/2 = 13 20 · 16 40 = 3 42 13 20,
E = 4 30 + 8 + 6 40 + 7 30 = 26 40,
A1 = E1 · A/E
= 4 30 · 3 42 13 20 / 26 40 = 4 30 · 8 20 = 37 30.
f = (23 20 - 10) / 13 20 = 13 20 / 13 20 = 1,
sq. d1 = sq. ha - f · 2 A1 = sq. 23 20 - 2 · 37 30 = 9 04 26 40 - 1 15 = 7 49 26 40,
d1 = 21 40, u1 = (ha - d1) / f = (23 20 - 21 40) / 1 = 1 40.
And so on, in three more steps of a geometric algorithm closely resembling the geometric algorithm which must have been used by the author of the orchard division text YBC 3879.
§10.2.6. Note that in all the three cited Old Babylonian examples the alternative trapezoid area rule is used directly, without first explicitly setting up and solving a quadratic equation or a rectangular-linear system of equations. As mentioned above, it is possible that the author of YBC 3879 = YOS 1, 24 proceeded in the same way, relying on a rule that he had learned in school. Unfortunately for him, relying on a ready-made area rule didn’t save him in any way from having to perform a long series of complicated numerical computations.
§11. Texts cited in the present paper
| museum no. | provenience | edition |
| 6N-T777 | Nippur | Zettler 1989: 311 |
| AO 5499 | Drehem | Nissen/Damerow/Englund 1990: 98 |
| AO 6060 | Umma | op.cit.: 65 |
| AO 7667 | Umma | Heimpel 2004 |
| AOT 304 | Girsu | Thureau-Dangin 1903: no. 413 |
| BM 104801 | unclear | Al-Rawi nd |
| BM 106425 | Umma? | Robson 2003/2004: 356 |
| BM 106444 | Umma? | loc.cit. |
| BM 111022 | unclear | Al-Rawi nd |
| BM 110387 | unclear | op.cit. |
| CMAA 16-C0005 | unclear | Friberg 2005: §2 |
| Erm 14645 | unclear | Koslova nd: 470 |
| HS 201 | Nippur | Oelsner 2001 |
| HSM 1659 | Girsu | Dunham 1986: 34 |
| IM 58045 | Nippur | Friberg 2007a: §11.3a |
| Ist Ni 2208 | Nippur | Proust 2007 |
| Ist Ni 5173 | Nippur | op.cit. |
| Ist O 1107 | Girsu | Friberg 2007b: ch. 5 |
| MS 1850 | unclear | op.cit.: ch. 5 |
| MS 1938/2 | unclear | op.cit.: §8.1.2 |
| MS 1984 | Umma | op.cit.: ch. 5 |
| MS 2792 | Uruk | op.cit.: ch. 10 |
| MS 3052 | unclear | op.cit.: ch. 10 |
| Plimpton 322 | Larsa | op.cit.: app. 8 |
| VAT 7029 | Drehem | Schneider 1930: no. 508 |
| VAT 7030 | Umma | op.cit.: no. 510 |
| YBC 3879 | Umma | Clay 1915: no. 24 |
| YBC 3901 | Umma | op.cit.: no. 23 |
| YBC 4675 | Larsa? | Friberg 2007a: 273 |
| Wengler 36 | Umma | Nissen/Damerow/Englund 1990:66 |
| 32 field plan texts | diverse | Liverani 1990 |
Bibliography
| Allotte de la Fuÿe, François M. | ||
| 1915 | “Un cadastre de Djokha.” RA 12, 47-54. | |
| Clay, Albert T. | ||
| 1915 | Miscellaneous Inscriptions in the Yale Babylonian Collection. YOS 1. New Haven: Yale University Press. | |
| Dunham, Sally S. | ||
| 1986 | “Sumerian words for foundation. Part I: Temen.” RA 80, 31-64. | |
| Friberg, Jöran | ||
| 1997 | ““Seed and Reeds Continued.” Another Metro-Mathematical Topic Text from Late Babylonian Uruk.” BagM 28, 251-365, plts. 45-46. | |
| 2001 | “Bricks and Mud in Metro-Mathematical Cuneiform Texts.” In J. Høyrup and P. Damerow, eds., Changing Views on Ancient Near Eastern Mathematics. Berlin: Max Planck Institute for the History of Science, pp. 61-154. | |
| 2005 | “On the Alleged Counting with Sexagesimal Place Value Numbers in Mathematical Cuneiform Texts from the Third Millennium B.C.,” Cuneiform Digital Library Journal 2005:2. | |
| 2007a | Amazing Traces of a Babylonian Origin in Greek Mathematics. Singapore: World Scientific. | |
| 2007b | A Remarkable Collection of Babylonian Mathematical Texts. Manuscripts in the Schøyen Collection: Cuneiform Texts 1. New York: Springer. | |
| 2009 | Review of Robson, Mathematics in Ancient Iraq: A Social History (2008). AfO 52 (forthcoming). | |
| Heimpel, Wolfgang | ||
| 2004 | “AO 7667 and the Meaning of ba-an-gi4.” Cuneiform Digital Library Journal 2004:1. | |
| Høyrup, Jens | ||
| 2002 | Lengths, Widths, Surfaces. A Portrait of Old Babylonian Algebra and its Kin. New York: Springer. | |
| Keiser, Clarence E. | ||
| 1919 | Selected Temple Documents of the Ur Dynasty. YOS 4. New Haven: Yale University Press. | |
| Koslova, Natalya | ||
| nd | Ur III Texts in the Hermitage Collection, vol. 3 | |
| Liverani, Mario | ||
| 1990 | “The shape of Neo-Sumerian fields.” BSA 5, 147-186. | |
| 1996 | “Reconstructing the rural landscape of the ancient Near East.” JESHO 39, 1-41. | |
| Neugebauer, Otto | ||
| 1929-31 | “Zur Geschichte der babylonischen Mathematik.” Quellen und Studien zur Geschichte der Mathematik 1, 67- 80. | |
| Neugebauer, Otto and Abraham Sachs | ||
| 1945 | Mathematical Cuneiform Texts. New Haven: American Oriental Society. | |
| Nissen, Hans J., Peter Damerow, and Robert K. Englund | ||
| 1993 | Archaic Bookkeeping, Early Writing and Techniques of Economic Administration in the Ancient Near East. Chicago: The University of Chicago Press. | |
| Oelsner, Joachim | ||
| 2001 | “HS 201 – Eine Reziprokentabelle der Ur III-Zeit.” In J. Høyrup and P. Damerow, eds., Changing Views on Ancient Near Eastern Mathematics. BBVO 19. Berlin: Max Planck Institute for the History of Science, pp. 53- 59. | |
| Proust, Christine | ||
| 2007 | Tablettes mathématiques de Nippur. Varia Anatolica XVIII, IFEA Georges-Dumezil. Paris: De Bocard. | |
| Quillien, Jacques | ||
| 2003 | “Deux cadastres de l’époque d’Ur III.” Revue d’Histoire des Mathématiques 9, 9-31. | |
| Robson, Eleanor | ||
| 1999 | Mesopotamian mathematics 2100-1600 BC: Technical Constants in Bureaucracy and Education. Oxford: Clarendon Press. | |
| 2003-04 | Review of J. Høyrup and P. Damerow, eds., Changing Views on Ancient Near Eastern Mathematics. BBVO 19. AfO 50, 356-362. | |
| 2008 | Mathematics in Ancient Iraq: A Social History. Princeton and Oxford: Princeton University Press. | |
| Schneider, Nicholas | ||
| 1930 | Die Geschäftsurkunden aus Drehem und Djoha. OrNS 47-49. | |
| Schuster, Hans-Siegfried | ||
| 1929-31 | “Quadratische Gleichungen der Seleukidenzeit aus Uruk.” Quellen und Studien zur Geschichte der Mathematik 1, 194-200. | |
| Zettler, Richard L. | ||
| 1989 | “Field plans from the Ur III temple of Inanna at Nippur.” ASJ 11, 305-313. | |
Version: 23 September 2009


