Keywords
Ur, ED I, proto-cuneiform, numbers, metrology
§1. Presentation of sources
§1.1 Origin and distribution of Ur archaic tablets
§1.1.1 The archaic tablets discussed here[1] were uncovered by joint excavations of the British Museum and the Philadelphia University Museum at Ur, in Southern Iraq, from 1926 till 1934.[2] This archaeological site, modern Tell al-Muqayyar, was excavated and studied by the archaeologist Sir Leonard Woolley,[3] who published his highly detailed results in a number of important papers.[4] He also wrote a popular work, in which he interprets the effects of the biblical flood in lower Mesopotamia, while trying to arouse the interest of the reader in the archaic city of Ur.[5] The archaic tablets of Ur were published in 1935 by Father Eric Burrows in UET 2.[6] Since that time, very few Assyriological studies have been devoted to these texts.[7]
§1.1.2 The tablets can be divided according to the season of their discovery and the archaeological strata, distinguished by the seals they contained (SIS =Seal Impression Strata), in which they were found (see figure 1 below). The famous “royal cemetery,” excavated by Woolley’s team and dated to the Early Dynastic period IIIa, is just above SIS V.[8] SIS I and SIS II are located immediately above the cemetery.
| Seasons | Tablets | Notes |
| 1926-1927 | nos. 1-13, 14 | In the first trenches of the cemetery excavation |
| nos. 308 and 310 | Not divided up according to SIS strata, which were only defined in 1929-1930 | |
| 1927-1928 | no. 15 | Probably from a level corresponding to SIS IV or V, according to Burrows" reconstruction. |
| 1928-1929 | nos. 16-235, 234 | Found in a level just over the cemetery, in SIS IV and V |
| no. 309 | SIS IV or V | |
| no. 373 | SIS IV or V | |
| 1929-1930 | nos. 236-304, 264, 299-301 |
SIS IV and V |
| no. 305 | SIS VII | |
| no. 306 | SIS VII | |
| no. 307 | SIS VIII | |
| (Burrows notes that these three tablets are similar to these found in SIS IV and V) | ||
| 1928-1930 | Seal impressions nos. 311-337 | SIS IV and V |
| 1932-1933 | nos. 339-372 | SIS IV and V |
Figure 1: Archaic tablets from Ur excavations
§1.1.3. The origin of tablet no. 338 is unknown (the document may have been found before 1926). The small number of tablets discovered during the 1931-1932 season was not yet available when Burrows was preparing the publication of UET 2. Other tablets were uncovered within the SIS I and II levels, and belong therefore to a period (Fara or Akkad period) later than the main collection. These were published as a supplement to the main volume of ED I texts. We note, therefore, that a large majority of the tablets constitute a homogeneous set, associated with SIS IV and V. The current study is based on the analysis of these documents, now to be found in the collections of three different museums: the British Museum in London, the Iraq Museum in Bagdad, and the University Museum in Philadelphia.
§1.2. Palaeographic observations
§ 1.2.1. Based on a preliminary classification of the tablets, Burrows listed the various signs impressed on their surfaces and also copied the tablets themselves (plates I-L of UET 2). A comparison of these copies with photographs of ten tablets that were available to me[9] shows that the accuracy of the copies is good, except for some details.[10] All the conclusions of this paper rest on Burrows’ copies, since it was not possible to work on the originals.
§ 1.2.2. Burrows argued that the ductus of these signs, of more or less rounded shape, seems to be situated at an intermediate stage between Jemdet Nasr and Fara documents. This point was confirmed by A. Falkenstein in his review article of UET 2.[11] Since Burrows’ work, very few studies have been devoted to the palaeography of Ur archaic texts, as emphasized by F. Pomponio.[12] P. Steinkeller classifies Ur archaic texts between those of Jemdet Nasr and Fara in his paleography of the sign TIL.[13] Another paleographic table published by Pomponio allows us, on the other hand, to observe some peculiarities concerning Ur archaic signs.[14] For example, the form ( ) of the sign NINDA and the form (
) of the sign NINDA and the form ( ) of the sign DA are not found in any other corpus. Furthermore, (ŠU) NIGIN2 does not appear on any tablet of UET 2. This term usually indicates “total”, or “sub-total,” corresponding to the sum of different quantities of products, during the later Early Dynastic period in other corpora.[15] The expression used at Ur is GU2 AN ŠE3, the same as that which represents “grand total” in ED III accounts.[16]
) of the sign DA are not found in any other corpus. Furthermore, (ŠU) NIGIN2 does not appear on any tablet of UET 2. This term usually indicates “total”, or “sub-total,” corresponding to the sum of different quantities of products, during the later Early Dynastic period in other corpora.[15] The expression used at Ur is GU2 AN ŠE3, the same as that which represents “grand total” in ED III accounts.[16]
§ 1.2.3. Other peculiarities concerning the archaic corpus of Ur can be noted. Burrows observed that 70% of the UET 2 documents have a flat obverse and a convex reverse, whereas 20% have two faces of roughly the same curvature.[17] In contrast, the Jemdet Nasr tablets have a convex obverse and a flat reverse. The asymmetric subdivisions of lines and columns which are characteristic of Late Uruk tablets are not found at Ur.[18] In fact, there are no documents that include “cases” divided into “sub-cases” in the Ur corpus. Some tablets even look like grids, as in Fara or Abu Salabikh.[19] This may show an inclination towards a formalization in tablet format. The scribe certainly must have had in mind a precise idea of the format of the tablet based on the products to be registered, before he began organizing the document into compartments and inscribing the signs.
Another peculiarity of these Ur texts lies in the writing of numerical signs. Some numerals were made with the round end of the stylus being impressed in the clay perpendicularly or at an angle. The others, however, were inscribed with a stylus cut in the shape of a rectangle. Here are some examples:
Rounded signs:

Rectangular signs

§1.2.4. The signs of the second type have never been the object of specific studies, and they are not included in the list established by H. J. Nissen and M. Green in ATU 2.[20] In ATU 5, R. K. Englund indicates that two tablets found at Uruk do in fact have signs of rectangular shape: tablets W 9579,an and W 6573,b.[21] M. Powell also makes a number of brief references to this type of sign, which he describes simply as a local variation in the way of inscribing metrological units.[22]
§ 1.2.5. The paleographical study of Ur texts is complex, primarily because of the lack of previous studies and research tools that deal with the subject. Such a study would have to consider the local scribal practices in lower Mesopotamia, and thus not presuppose the idea of a strictly linear and homogeneous development of writing in this region. R. D. Biggs has noted that it is indeed difficult to understand clearly whether paleographical disparities during this period are due to chronological or geographical factors.[23]
§2. Archaic metrological systems from Ur
§ 2.1. Methodology
§ 2.1.1. In order to identify metrological systems, it is first necessary to throw light on numerical signs which may correspond to metrological units, and then to reconstruct, if possible, the relations between these units.
§ 2.1.2. Two principles were strictly adhered to. First of all, the numerical signs within a particular compartment of a tablet are registered before any other signs. One or two styli, the ends of which were wider than those typically used, were employed to inscribe marks in the shape of easily recognizable strokes. Secondly, units were registered in decreasing order. These indications thus make the identification of numerical signs possible.
§ 2.1.3. With such a collection of correspondences in hand, the easiest way to proceed is to gather evidence of the succession of units as well as the relations between them. In this respect the work of the “Berlin Workshop” on the Uruk and Jemdet Nasr texts has provided an essential set of results[24]: metrological units are strictly dependent on registered products, and the same sign can be found in two or more different systems. Semantic fields can be reconstructed in which particular terms play some role as semantic indicators. In the course of my research, I have established five categories in Ur texts of the ED I period, namely: “area,” “cereals,” “livestock,” “wood” and “containers”. These intentionally broad numerical groups are described in the sections 2.2.1-5 below, in each case where relevant including both curvilinear and rectangular graphemes.
§ 2.1.4. The set of “cereals,” for example, concerns any kind of grain and its by-products. Once tables covering the set of all relevant numerical combinations are established, the metrological systems linked to the previously identified categories can be reconstructed. The next step consists of the comparison of each of the systems to all of the other systems, category by category. Some patterns of numerical signs were shown to be identical, while others were incompatible, but it would have been premature to stop the work at this stage. One might have gone away with the impression that each category of items had its own metrological system, used strictly for elements of that category. This phenomenon, however, does not occur in the Uruk and Jemdet Nasr texts. For example, the same numerical system is used for the accounting of grain rations and for quantities of fresh fish. It is thus necessary to leave aside arbitrary classifications in order to be able to compare the different systems which can be established and to track down those that are identical.
§ 2.2. Metrological diagrams
§ 2.2.0. The results of this “transverse” synthesis allows for the accumulation of metrological indications for different categories according to analogies in the succession and the shape of the units. These indications are best represented in metrological diagrams, the principle of which has been established by J. Friberg[25]; sign identifiers and orientation follow the standards established in ATU 2, 335-345. Units are registered in decreasing order, and relations between them are indicated by means of arrows.
§2.2.1. Group 1
“Area 1 system: curvilinear signs”

“ Area 3 system: rectangular signs”

§2.2.1 bis. Group 1 (bis)
“ Area 2 system: curvilinear signs”

§2.2.2. Group 2
“ Cereal 1 system: curvilinear signs”

“Cereal 1 system (bis): curvilinear signs”

“ Cereal 1 system: rectangular signs”

§2.2.3. Group 3
“ Cereal 2 system: curvilinear signs”

“ Cereal 2 system: rectangular signs”

“ Containers 2 system: curvilinear signs”

“ Containers 3 system: curvilinear signs”

§2.2.4. Group 4
“ Cereal 3 system: rectangular signs”

“ Wood system: rectangular signs”

“ Containers 1 system: curvilinear signs”

“ Containers 7 system: curvilinear signs”
System with the following units:

§2.2.5. Group 5
“ Cereals 4 system: rectangular signs”

“ Livestock system: rectangular signs”

“ Containers 4 system: curvilinear signs”
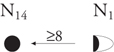
“ Containers 5 system: rectangular signs”

“ Containers 6 system: curvilinear signs”

§ 2.2.6. If the diagrams of each group correspond in each case to a single system, we may conclude that at least six archaic metrological systems were in use at Ur during the Early Dynastic I period.[26] Some groups include metrological diagrams associated with several categories:
| Group 1 | →→→→ | “area” category |
| Group 1 (bis) | →→→→ | “area” category |
| Group 2 | →→→→ | “cereals” category |
| Group 3 | →→→→ | “cereals” category |
| →→→→ | “containers” category | |
| Group 4 | →→→→ | “cereals” category |
| →→→→ | “wood” category | |
| →→→→ | “containers” category | |
| →→→→ | “livestock” category | |
| Group 5 | →→→→ | “cereals” category |
| →→→→ | “livestock” category | |
| →→→→ | “containers” category |
§2.3. Synthesis
§ 2.3.1. Significant results have been gained through the study of each category. The analysis of numerical sign combinations attested on tablets concerning area measures of fields allowed the elaboration of several diagrams showing the relations between the different units. But the exact algebraic relation between two particular consecutive units cannot be exactly determined. However, their order in succession has been demonstrated. We do note graphical and numerical similarities between systems “area” 1-3. Even though round and rectangular signs certainly represent graphical variants of identical units, and in spite of the strong similarities between “area” 1 and “area” 3 systems, the sign with two concentric discs (![]() , notated N50[27]) remains problematic. It never appears in any numerical combination with the sign with a single disc (
, notated N50[27]) remains problematic. It never appears in any numerical combination with the sign with a single disc (![]() , notated N45). Consequently, the following hypothesis, already suggested by Burrows and Nissen, should be considered: the sign N50 may well be strictly equivalent, within the framework of the same metrological system, to sign N45. “Area” 1 and 2 systems would be identical. Furthermore, if the “Area” 3 system is equivalent to the “area”1 system, we can notice that no unit represented by a square inside a big square and corresponding to sign N50 belongs to it. The square sign equivalent to the sign N45 would represent the same unit as N50 in the same metrological system, i.e., the system dealing with area measures of fields.
, notated N45). Consequently, the following hypothesis, already suggested by Burrows and Nissen, should be considered: the sign N50 may well be strictly equivalent, within the framework of the same metrological system, to sign N45. “Area” 1 and 2 systems would be identical. Furthermore, if the “Area” 3 system is equivalent to the “area”1 system, we can notice that no unit represented by a square inside a big square and corresponding to sign N50 belongs to it. The square sign equivalent to the sign N45 would represent the same unit as N50 in the same metrological system, i.e., the system dealing with area measures of fields.
§ 2.3.2. But the hypothesis of a single numerical system raises questions which cannot be answered at present. Both graphical and numerical analogies point to a close relation with the GAN2 system concerning areas of fields in the older tablets from Uruk and Jemdet Nasr. However, signs N45 and N50, which represent units of the GAN2 system, are clearly distinguished. The first unit is equivalent to six times the second. Why did the scribes of Ur give up such a system which had been used regularly during the previous periods? Why would the units N45 and N50 no longer be distinguished? Why was the sign N50 occasionally inscribed when it would have been simpler to use the sign N45 every time, since it only requires a single stylus? Why finally are identical units of this system indicated with different graphic variants (round signs as opposed to rectangular signs)?
§ 2.3.3. The term GU2 AN ŠE3 does not seem to have been used before our Ur documents. Unfortunately, the occurrences of the sign combination GU2 AN ŠE3 qualifying a total in the Ur texts are, due to the tablets’ poor state of preservation, of little use in reconstructing metrological systems related to plots of land. The term does appear in texts from later periods, and is attested in the following ED I Ur accounts: nos. 21, 85, 97, 113d, 122, 127, 147bis, 163, 164, 166, 184, 297, 356, 359, 365, and 371. Six of these tablets are classified in the “field” category: nos. 127, 147bis, 164, 184, 356, and 365. When it is inscribed on a single surface, GU2 AN ŠE3 is written next to a large combination of numerical signs (corresponding to the presence of quantitatively large units); see nos. 147bis and 365. When tablets are inscribed on both faces, GU2 AN ŠE3 appears on the reverse. Unfortunately, tablets nos. 164, 184 and 356 are partially damaged, and it is difficult to determine whether the combination of the associated numerical signs on the reverse corresponds to the total of the combinations on the obverse.
§ 2.3.4. The study of tablets that deal with cereals and the products produced from them seems more complex. The specificity of the relevant foodstuffs has to be considered, and it is necessary to presume that these foodstuffs were not necessarily all registered in the same system. A large variety of numerical signs associated with these foodstuffs can be observed in the accounts: round and rectangular signs, streaked or not. Links between different units seem then more difficult to discern. But, in contrast with documents registering fields, there are tablets which are preserved well enough to allow the reconstruction of “totals”—that is, sums of particular available quantities: tablets nos. 21, 83, and 185. Therefore, clear relations between units can be defined. In particular, units represented by different diacritical signs (streaked and not streaked) can be added together. Furthermore, the hypothesis according to which, in the “area” category, the term GU2 AN ŠE3 stands for a “total,” a “sum” of different quantities has been confirmed. There are several numerical systems associated with cereals. The data is not clear enough to establish their number, but at least four different systems can be identified: systems “cereals” 1-4. In spite of some disparities, systems “cereals” 1-4 apparently correspond to some proto-cuneiform systems studied by the Berlin ATU group.[28]
§ 2.3.5. But new questions were also raised. It is indeed difficult to identify the metrological system in which some of the products are registered. For example, ŠE NINDA2׊IM is associated with at least two different systems. Other foodstuffs, such as AŠ2 or KAL GAR, are associated with both round signs and rectangular signs, streaked and not streaked. The reconstruction of the totals shows that the units of the “cereals” 1 system can be subsumed in those of the “cereals” 2 system. But what is the difference between these two systems? What information is carried by streaked signs as opposed to the signs which are not streaked? Why are some products indifferently associated with the both types of graphic signs? We have to suppose that either the product represented by the sign combination KAL GAR was registered by means of two different systems, or there were at least two different systems made up of streaked signs.
§ 2.3.6. There are not as many numerical combinations associated with animals. Nevertheless, at least two distinct numerical systems seem to have been used in order to register them. The first one, associated with breeding animals, may correspond to a system often used for the same purpose during the Uruk and Jemdet Nasr periods. But it should be noted that the units which make it up are represented by rectangular signs, except on tablets nos. 151 and 252. Because of the units’ succession, this “containers” 1 system may be equivalent to the “cereals” 4 system attested for the grain category.
§ 2.3.7. If the “wood” system which is used for wooden objects is in fact identical to the “cereals” 3 and “containers” 7 systems, which are used with cereals and fish respectively, it may also be a possible equivalent of the so called “bisexagesimal” system as defined by the Berlin proto-cuneiform group.[29] All the commodities registered with this “wood” system belong to a system of rations, but what kind of rations can be associated with objects made of wood or reed? Are they themselves bowls or containers for special quantities of foodstuffs?
§ 2.3.8. It is impossible to discern exactly which metrological systems are associated with products containing the indicator DUG in the “containers” category. We must simply suppose that DUG, which appears on tablets with ŠE GAR and KAL GAR, can be registered with the same system as these two foodstuffs. But how can we explain the fact that DUG appears also along with streaked signs? We have already encountered this problem with the attestations of KAL GAR in the “cereals” category. Is DUG registered in two different numerical systems?
§ 3. Conclusion
§ 3.1. By means of cross-categorial comparisons, it has been possible to produce a classification of the metrological systems attested with items of all categories into five distinct groups.[30] Consequently, we may argue that, at Ur in the archaic period, at least five metrological systems were in use, and not, as Burrows[31] and Wright[32] thought, only three. Furthermore, these systems were not always associated with a single specific foodstuff. For example, if the “cereals” 3, “wood”, and “containers” 1 and 7 systems of group 4 represent only one system, this single system would allow for the registration and quantification of products linked to cereals, animals, wood and recipients.
§ 3.2. This short study leaves many unanswered questions. The notation of units belonging to different metrological systems is one of the characteristics of the writing system at Ur. The scribes used either round or rectangular signs. However, it is interesting to observe that rectangular signs are no longer attested in the texts dated to later periods. The two signs types stood for the same units in different metrological systems: the “area” 1 and 3 systems; the “cereals” 1 round sign system and the “cereals” 1 rectangular sign system; the “cereals” 2 round sign system and the “cereals” 2 rectangular sign system. What is the scope of this graphical distinction made by the scribes from Ur in the writing of units? This choice may be based on the deliberate use of a new stylus, the end of which was cut so as to inscribe rectangular signs. It is necessary to try to characterize the economic, cultural or other factors which influenced its use. But this problem is rather complex. Some tablets include both cuneiform and curvilinear signs. What was the purpose of this clear distinction of the scribe?
§ 3.3. Another problem is raised by the use of streaked signs. The units represented by means of these signs can be added to those of the “cereals” 1 rectangular sign system. But units of this system are usually symbolized by non-streaked signs. Additional information about the types of cereal, or their methods of processing, may thus be provided by such incisions on the signs.
§ 3.4. Metrological systems at Ur are also distinct from those of the previous periods. In the Jemdet Nasr texts, as well as in the later texts, the use of the unit represented by the sign N50 is clearly attested in the GAN2 system concerning measures of areas. Nevertheless, the inclusion, at Ur, of this unit in the “area” 1 system, which seems to resemble the proto-cuneiform GAN2 system, is not entirely certain.
§ 3.5. It is difficult to identify factors which explain these disparities in the composition of the metrological systems and the graphical representations of units. But, for reasons which are unclear at the moment, the metrological systems in use at the time of Uruk and Jemdet Nasr periods were not resumed without changes at Ur. Their use and modifications are to be studied as part of the economic and political context to which they belong.
Notes
1 I want to thank G. Cifoletti and J. Ritter who were the first academic referees of the work on which this article is based. Grateful acknowledgement is also made to J.-M. Durand, B. Foster, J. Friberg and especially B. Lafont and R. K. Englund for their many helpful comments.
2 The tablets will be designated in this paper by their publication number.
3 S. L. Woolley, Ur Excavations II: The Royal Cemetery (London: The British Museum and the University Museum, University of Pennsylvania, 1936); S. L. Woolley, Ur Excavations IV: The Early Periods (London: The British Museum and the University Museum, University of Pennsylvania, 1956).
4 Antiquaries Journal 10 (1930) 327-337; for the papers about Woolley’s work, see E. L. Mallowan, Iraq 22 (1960) 1-19.
5 S. L. Woolley, Ur of the Chaldees: A Record of Seven Years of Excavation (London 1929, revised edition 1954).
6 E. Burrows, Ur Excavations Texts II: Archaic Texts (London: The British Museum and the University Museum, University of Pennsylvania, 1935).
7 In chronological order: I. Golgher, “La structure économique et sociale de Sumer présargonique II,” Thèse pour obtenir le diplôme de l’Ecole des Hautes Etudes (Section IV) à la Sorbonne (Paris 1959); H. J. Nissen, Zur Datierung des Königsfriedhofes von Ur (Bonn 1966); H. T. Wright, The Administration of Rural Production in an Early Mesopotamian Town (=Museum of Anthropology, University of Michigan no. 38; Ann Arbor 1969); P. Charvat, “Early Ur,” ArOr 47 (1979) 15-20; P. Charvat, “Early Ur-War Chiefs and Kings of Early Dynastic III,” AoF 9 (1982) 43-59; J. Bauer, “Ortsnamen in den frühen Texten aus Ur ,” WO 18 (1987) 5-6; P. Steinkeller, “Grundeigentum in Babylonien von Uruk IV zur frühdynastischen Period II,” in Das Grundeigentum in Mesopotamien, Jahrbuch für Wirtschaftsgeschichte (Berlin 1988) 11-27.
8 S. L. Woolley, Ur Excavations II: The Royal Cemetery.
9 Tablets nos. 24, 68b, 73, 87, 90, 122, 133, 183, 188 and 218. I would like to thank the Trustees of the British Museum and the University Museum of the University of Pennsylvania for having provided me with these photos, and in particular J. Ritter who acted as intermediary.
10 For example, in tablet no. 87, the signs inscribed by Burrows in obv. iii 1 are not two notches with two “circles” but four notches. The signs which he has copied in i 1 of the tablet no. 122 are not visible on the photo (the tablet is very damaged).
11 A. Falkenstein, “Keilschriftforschung: Ur Excavations Texts II von E. Burrows,” OLZ 2 (1937) 95.
12 F. Pomponio and A. Alberti, Pre-Sargonic and Sargonic Texts from Ur edited in UET 2. Supplement (=Studia Pohl Series Maior 13; Rome: Biblical Intitute Press, 1986) p. 9. Pomponio studied the evolution of ten signs (BA, DA, DI, E2, IGI, KA, MU, NINDA, PA, ŠE and ŠU-NIGIN2) in texts from eight different sites: Ur, Fara, Abu Salabikh, Ebla, Lagash, Adab, Nippur and Zabala.
13 P. Steinkeller, “Studies in Third Millennium Paleography 1: Signs TIL and BAD,” ZA 71 (1981) 19-28.
14 Ibid., table A on p. 13.
15 For example, in the texts from ED IIIb Lagash.
16 See R. D. Biggs, OIP 99, p. 44, fn. 8, for further discussion of this phrase.
17 UET 2, p. 4.
18 The formats of the Jemdet Nasr and Late Uruk texts have been dealt with by R. K. Englund and J.-P. Grégoire in The Proto-Cuneiform Texts from Jemdet Nasr (=MSVO 1; Berlin 1991) pp. 10-12, and Englund in J. Bauer, R. K. Englund, M. Krebernik, Mesopotamien: Späturuk-Zeit und Frühdynastische Zeit (=OBO 160/1; Freiburg, Switzerland, 1998) pp. 56-64, respectively.
19 Tablets UET 2, nos. 22, 30, 234, 252 and 283.
20 M. W. Green and H. J. Nissen, Zeichenliste der Archaischen Texte aus Uruk (=ATU 2; Berlin, 1987).
21 R. K. Englund, ATU 5, p. 31. Englund argues that the second tablet is to be dated to the Early Dynastic periods I or II, because the “rectangular shaped signs” are very common in the archaic texts from Ur.
22 M. A. Powell, “Sumerian Area Measures and the Alleged Decimal Substratum,” ZA 62 (1972) 171.
23 R. D. Biggs, “On Regional Cuneiform Handwriting in Third Millennium Mesopotamia,” OrNS 42 (1973) 39-46 as well as M. Lambert, RA 53 (1959) 218.
24 Many scholars have taken part in the “Berlin Workshop” at one time or another: P. Damerow, R. K. Englund, J. Friberg, J. Høyrup, M. Powell , H. Nissen and J. Ritter. See Høyrup’s introduction to the volume J. Høyrup and Peter Damerow, eds., Changing Views on Ancient Near Eastern Mathematics(=BBVO 19; Berlin, 2001) vii-xvi.
25 J. Friberg, The Third Millennium Roots of Babylonian Mathematics I ; A Method for the Decipherment, throught Mathematical and Metrological Analysis of Proto-Sumerian and Proto-Elamite Semi-Pictographic Inscriptions (Department of Mathematics, The University of Göteborg, 1979).
26 The minimal number is possibly 5, if the systems “area” 1 and 2 are identical, but this hypothesis is very uncertain.
27 Despite the cumbersome notations chosen by the Berlin project ATU to identify numerical signs, it is important to avoid unnecessary confusion by accepting “Nn” as convention in future discussions of archaic texts.
28 ATU 2, 136-141.
29 ATU 2, 132-135.
30 I have established six groups, but I am not sure that systems “area” 1 and 2 can be clearly dissociated.
31 UET 2, plts. 35-37.
32 Rural Production p. 100.
Version: 23 December 2003


